 B .
B .  C .
C .  D .
D . 
 C .
C .  D .
D . 
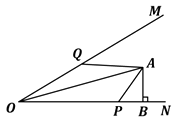
如图, 平分
,
于点
,
,点 P从
出发,以
的速度沿线段
向终点
运动;同时,点
从
出发,以
的速度沿射线
运动,当点 P到达终点
时,则两点均停止运动. 那么经过
,能使
.
②若 ,则
°.
定义:三角形三条内角平分线的交点叫做三角形的内心;
性质:内心到三角形三边的距离相等.
如图1,点 为
的内心,
于
,
于E,
于
,则有
.
问题:如何求 的值呢?
探究:
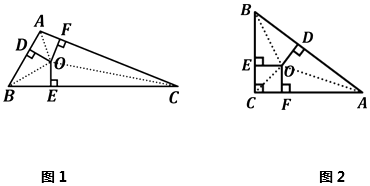
①图1中, ,
,
,
,请你根据小明的思路求出
的值;
②如图2,△ABC中, ,设
,
,
,
为 △ABC的内心,
于
,
于E,
于
.若设
,请用含
,
,
的式子表示
;
②应用:已知一个直角三角形的两直角边长分别为 和
,求该三角形的内心到任意一边的距离
.