2017年江西省赣州市石城县中考数学一模试卷

更新时间：2017-04-20 浏览次数：576 类型：中考模拟

一、选择题

1. (2017·石城模拟) 下列图形中，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2017·石城模拟) 下列运算中，正确的是（）

A . m²×m³=m⁶ B . （m³）²=m⁵ C . m+m²=2m³ D . ﹣m³÷m²=﹣m

答案解析收藏纠错 + 选题
3. (2017·石城模拟) 已知m，n是一元二次方程x²﹣4x﹣3=0的两个实数根，则代数式（m+1）（n+1）的值为（）

A . ﹣6 B . ﹣2 C . 0 D . 2

答案解析收藏纠错 + 选题
4. (2019九上·深圳期末) 如图是一个底面为正方形的几何体的实物图，则其俯视图为（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2017·石城模拟) 如图，在△ABC中，∠C=90°，将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，已知MN∥AB，MC=6，NC= $\text{[math]}$ ，则四边形MABN的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2017·石城模拟) 已知二次函数y=ax²+bx+c（a≠0）与x轴交于点（x₁ ， 0）与（x₂ ， 0），其中x₁＜x₂ ，方程ax²+bx+c﹣a=0的两根为m、n（m＜n），则下列判断正确的是（）

A . m＜n＜x₁＜x₂ B . m＜x₁＜x₂＜n C . x₁+x₂＞m+n D . b²﹣4ac≥0

答案解析收藏纠错 + 选题

二、填空题

7. (2019九下·东台月考) 当分式 $\text{[math]}$ 的值为0时，x的值是．

答案解析收藏纠错 + 选题
8. (2017·石城模拟) 已知a+b=8，a﹣b=4，则a²﹣b²=．

答案解析收藏纠错 + 选题
9. (2017·石城模拟) 如图，已知二次函数y=x²+bx+c的图像的对称轴是直线x=1，过抛物线上两点的直线AB平行于x轴，若点A的坐标为（0， $\text{[math]}$ ），则点B的坐标为．

答案解析收藏纠错 + 选题
10. (2022·新会模拟) 如图，在半径为5的⊙O中，弦AB=6，点C是优弧 $\text{[math]}$ 上一点（不与A，B重合），则cosC的值为．

答案解析收藏纠错 + 选题
11. (2017·石城模拟) 如图，正方体的棱长为a，沿着共一个顶点的三个正方形的对角线裁截掉一个几何体之后，截面△ABC的面积=．

答案解析收藏纠错 + 选题
12. (2017·石城模拟) 以线段AC为对角线的四边形ABCD（它的四个顶点A、B、C、D按顺时针方向排列），已知AB=BC=CD，∠ABC=100°，∠CAD=40°；则∠BCD的大小为．

答案解析收藏纠错 + 选题

三、解答题

13. (2017·石城模拟) 根据题意解答
1. （1）计算：|﹣ $\text{[math]}$ |+（π﹣3）⁰+（ $\text{[math]}$ ）^﹣¹﹣2cos45°
2. （2）若关于x的一元二次方程x²+（k+3）x+k=0的一个根是﹣2，求方程的另一个根．
答案解析收藏纠错 + 选题
14. (2023八下·浏阳期末) 四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．
1. （1）求证：△ADE≌△ABF；
2. （2）若BC=8，DE=6，求△AEF的面积．
答案解析收藏纠错 + 选题
15. (2017·石城模拟) 如图，在3×3的方阵图中，填写了一些数和代数式（其中每个代数式都表示一个数），使得每行的3个数、每列的3个数、斜对角的3个数之和均相等．
3
4
x
﹣2
y
a
2y﹣x
c
b
备用图
3
4

﹣2
1. （1）求x，y的值；
2. （2）在备用图中完成此方阵图．
答案解析收藏纠错 + 选题
16. (2017·石城模拟) 如图，由6个形状、大小完全相同的小矩形组成大矩形网格，小矩形的顶点称为这个矩形网格的格点，请仅用无刻度直尺在矩形中完成下列画图．
1. （1）在图1中画出一个顶点均在格点上的非特殊的平行四边形；
2. （2）在图2中画出一个顶点均在格点上的正方形．
答案解析收藏纠错 + 选题
17. (2017·石城模拟) 小明家客厅里装有一种三位单极开关，分别控制着A（楼梯）、B（客厅）、C（走廊）三盏电灯，在正常情况下，小明按下任意一个开关均可打开对应的一盏电灯，既可三盏、两盏齐开，也可分别单盏开．因刚搬进新房不久，不熟悉情况．
1. （1）若小明任意按下一个开关，则下列说法正确的是（）
  
  A . 小明打开的一定是楼梯灯； B . 小明打开的可能是卧室灯； C . 小明打开的不可能是客厅灯； D . 小明打开走廊灯的概率是 $\text{[math]}$
2. （2）若任意按下一个开关后，再按下另两个开关中的一个，则正好客厅灯和走廊灯同时亮的概率是多少？请用树状图法或列表法加以说明．
答案解析收藏纠错 + 选题
18. (2017·石城模拟)
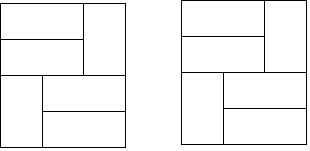
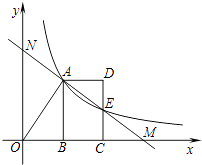
反比例函数y= $\text{[math]}$ （x＞0）的图像经过线段OA的端点A，O为原点，作AB⊥x轴于点B，点B的坐标为（2，0），tan∠AOB= $\text{[math]}$ ，将线段AB沿x轴正方向平移到线段DC的位置，反比例函数y= $\text{[math]}$ （x＞0）的图像恰好经过DC的中点E．
1. （1）求k的值和直线AE的函数表达式；
2. （2）若直线AE与x轴交于点M、与y轴交于点N，请你探索线段AN与线段ME的大小关系，写出你的结论并说明理由．
答案解析收藏纠错 + 选题
19. (2017·石城模拟) 某地区为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行加价收费．为更好地决策，自来水公司随机抽取部分用户的用水量数据，并绘制了如下不完整的统计图（每组数据包括右端点但不包括左端点），请你根据统计图解答下列问题：
1. （1）此次调查抽取了多少用户的用水量数据？
2. （2）补全频数分布直方图，求扇形图中“15吨～20吨”部分的圆心角的度数；
3. （3）如果自来水公司将基本用水量定为每户25吨，那么该地区20万用户中约有多少用户的用水全部享受基本价格？
答案解析收藏纠错 + 选题
20. (2017·石城模拟) 图1是安装在斜屋面上的热水器，图2是安装该热水器的侧面示意图．已知，斜屋面的倾斜角为25°，长为2.1米的真空管AB与水平线AD的夹角为40°，安装热水器的铁架水平横管BC长0.2米，求
1. （1）真空管上端B到AD的距离（结果精确到0.01米）；
2. （2）铁架垂直管CE的长（结果精确到0.01米）．
答案解析收藏纠错 + 选题
21. (2017·石城模拟) 在平面直角坐标系xOy中，已知点A（6，0），点B（0，6），动点C在以半径为3的⊙O上，连接OC，过O点作OD⊥OC，OD与⊙O相交于点D（其中点C、O、D按逆时针方向排列），连接AB．
1. （1）当OC∥AB时，∠BOC的度数为；
2. （2）连接AC，BC，当点C在⊙O上运动到什么位置时，△ABC的面积最大？并求出△ABC的面积的最大值；
3. （3）连接AD，当OC∥AD时，①求出点C的坐标；②直线BC是否为⊙O的切线？请作出判断，并说明理由．
答案解析收藏纠错 + 选题
22. (2017·石城模拟) 探究与应用．试完成下列问题：
1. （1）如图①，已知等腰Rt△ABC中，∠C=90°，点O为AB的中点，作∠POQ=90°，分别交AC、BC于点P、Q，连结PQ、CO，求证：AP²+BQ²=PQ²；
2. （2）如图②，将等腰Rt△ABC改为任意直角三角形，点O仍为AB的中点，∠POQ=90°，试探索上述结论AP²+BQ²=PQ²是否仍成立；
3. （3）通过上述探究（可直接运用上述结论），试解决下面的问题：如图③，已知Rt△ABC中，∠C=90°，AC=6，BC=8，点O为AB的中点，过C、O两点的圆分别交AC、BC于P、Q，连结PQ，求△PCQ面积的最大值．
答案解析收藏纠错 + 选题
23. (2017·石城模拟) 对于二次函数y=x²﹣3x+2和一次函数y=﹣2x+4，把y=t（x²﹣3x+2）+（1﹣t）（﹣2x+4）称为这两个函数的“再生二次函数”，其中t是不为零的实数，其图像记作抛物线E，现有点A（2，0）和抛物线E上的点B（﹣1，n），请完成下列任务；
1. （1）【尝试】①当t=2时，抛物线y=t（x²﹣3x+2）+（1﹣t）（﹣2x+4）的顶点坐标为
2. （2） ②判断点A是否在抛物线E上；
3. （3） ③求n的值．
4. （4）【发现】通过（2）和（3）的演算可知，对于t取任何不为零的实数，抛物线E总过定点，坐标为．
5. （5）
  【应用】
  ①二次函数y=﹣3x²+5x+2是二次函数y=x²﹣3x+3和一次函数y=﹣2x+4的一个“再生二次函数”吗？如果是，求出t的值；如果不是，说明理由；
  ②以AB为边作矩形ABCD，使得其中一个顶点落在y轴上；若抛物线E经过A，B，C，D其中的三点，求出所有符合条件的t的值．
答案解析收藏纠错 + 选题