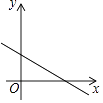 B .
B . 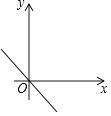 C .
C . 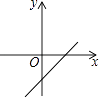 D .
D . 
①抛物线过原点;
②4a+b+c=0;
③a﹣b+c<0;
④抛物线的顶点坐标为(2,b);
⑤当x<2时,y随x增大而增大.
其中结论正确的是( )
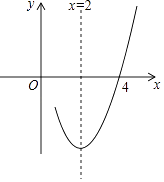

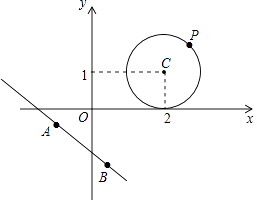
在平面直角坐标系xOy中,点P(x0 , y0)到直线Ax+By+C=0的距离公式为:d= .
例如:求点P0(0,0)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知,A=4,B=3,C=﹣3,
∴点P0(0,0)到直线4x+3y﹣3=0的距离为d= =
.
根据以上材料,解决下列问题: