 B .
B .  C .
C .  D .
D . 如图,反比例函数y= (x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )



国家环保局统一规定,空气质量分为5级.当空气污染指数达0﹣50时为1级,质量为优;51﹣100时为2级,质量为良;101﹣200时为3级,轻度污染;201﹣300时为4级,中度污染;300以上时为5级,重度污染.泰州市环保局随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:

某课桌生产厂家研究发现,倾斜12°﹣24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1所示,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30cm.

如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长.

如图3,当∠BAC=12°,求AD的长(结果保留根号).
[参考数据:sin24°=0.40,cos24°=0.91,tan24°=0.46,sin12°=0.20]

小平所在的学习小组发现,车辆转弯时,能否顺利通过直角弯道的标准是,车辆是否可以行驶到和路的边界夹角是45°的位置(如图1中 ②的位置).例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,即车辆能通过.

小平提出将拐弯处改为圆弧( 和
是以O为圆心,分别以OM和ON为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子?

如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.

如图1,在平面直角坐标系xOy中,已知点A(a,0)(a>0),B(2,3),C(0,3).过原点O作直线l,使它经过第一、三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
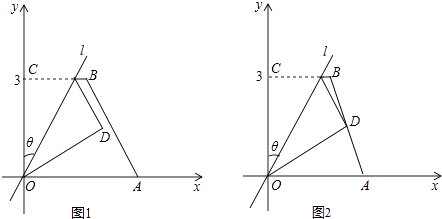
若点D与点A重合,则这个操作过程为FZ[,];
若点D恰为AB的中点(如图2),求θ;
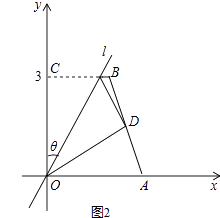
经过FZ[θ,a]操作后,作直线CD交x轴于点G,交直线AB于点H,使得△ODG与△GAH是一对相似的等腰三角形,直接写出FZ[θ,a].