
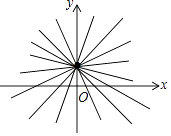
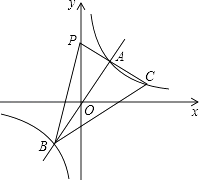
当k取不同的值时,y关于x的函数y=kx+1(k≠0)的图象为总是经过点(0,1)的直线,我们把所有这样的直线合起来,称为经过点(0,1)的“直线束”.那么,下面经过点(﹣1,1)的直线束的函数式是( )
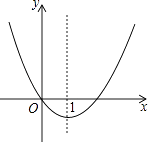
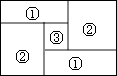
如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
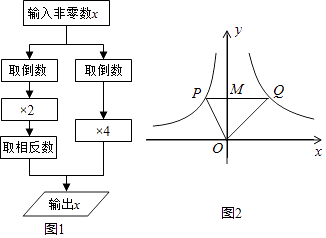
根据图1的程序,得到了y与x的函数图象,如图2,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ,则下列结论:①x<0时,y= ;②△OPQ的面积为定值;③x>0时,y随x的增大而增大;④MQ=2PM;⑤∠POQ可以等于90°.其中正确的有( )
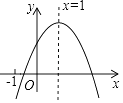
x | … | 1 | 2 | 3 | 4 | 5 | … |
y | … | 0 | ﹣3 | ﹣6 | ﹣6 | ﹣3 | … |
从上表可知,下列说法中正确的有( )
① =6;②函数y=ax2+bx+c的最小值为﹣6;③抛物线的对称轴是x=
;④方程ax2+bx+c=0有两个正整数解.
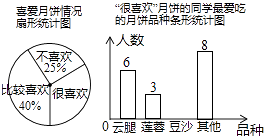
(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)
请根据统计图完成下列问题:
条形统计图中,喜欢“豆沙”月饼的学生有人;

请回答下列问题:
(参考数据:sin18°≈0.31,cos18°≈0.95.tan18°≈0.32,sin36°≈0.59.cos36°≈0.81,tan36°≈0.73)
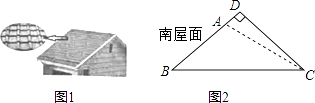
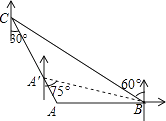
如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120海里.
如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
如图2,
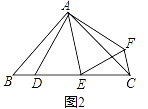
在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
如图3,
若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
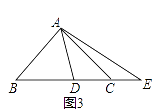
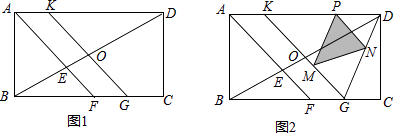
若KD=KG,BC=4﹣ .
①求KD的长度;
②如图2,点P是线段KD上的动点(不与点D、K重合),PM∥DG交KG于点M,PN∥KG交DG于点N,设PD=m,当S△PMN= 时,求m的值.
如图1,已知平行四边形ABCD顶点A的坐标为(2,6),点B在y轴上,且AD∥BC∥x轴,过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),点F(m,6)是线段AD上一动点,直线OF交BC于点E.
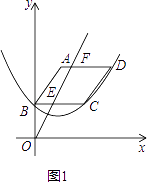
如图2,过点F作FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,垂足为N,连接MN,直线AC分别交x轴,y轴于点H,G,试求线段MN的最小值,并直接写出此时m的值.