①对顶角的平分线;②邻补角的平分线;③平行线截得的一组同位角的平分线;④平行线截得的一组内错角的平分线;⑤平行线截得的一组同旁内角的平分线.
⑴两条直线相交于一点有2组不同的对顶角;
⑵三条直线相交于一点有6组不同的对顶角;
⑶四条直线相交于一点有12组不同的对顶角;
⑷n条直线相交于同一点有组不同对顶角.(如图所示)

如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
求证:CF∥DO.

证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°()
∴DE∥BO()
∴∠EDO=∠DOF()
又∵∠CFB=∠EDO()
∴∠DOF=∠CFB()
∴CF∥DO()
某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:


②若 ,则x的取值范围是.
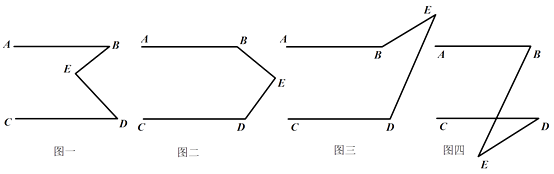
有一天李明同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图一),他用鼠标左键点住点E,拖动后,分别得到如图二,三,四等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着李明同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.