(Ⅰ)求角C的值;
(Ⅱ)若c=2,且△ABC为锐角三角形,求a+b的取值范围.

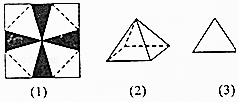
(Ⅰ)求证:PC⊥AB;
(Ⅱ)求证:平面PAB⊥平面ABC;
(Ⅲ)求二面角B﹣AP﹣C的余弦值.
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 5 | ||
女 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为 .
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;
(Ⅲ)已知在患心肺疾病的10位女性中,有3位又患胃病.现在从患心肺疾病的10位女性中,选出3名进行其他方面的排查,记选出患胃病的女性人数为ξ,求ξ的分布列,数学期望以及方差;大气污染会引起各种疾病,试浅谈日常生活中如何减少大气污染.
下面的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式K2= 其中n=a+b+c+d)
(Ⅰ)若 ,求椭圆的方程;
(Ⅱ)设直线y=kx与椭圆相交于A,B两点,M,N分别为线段AF2 , BF2的中点.若坐标原点O在以MN为直径的圆上,且 ,求k的取值范围.
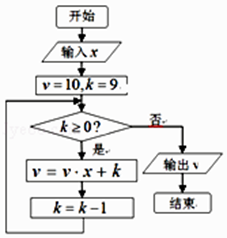
(Ⅰ)求a,b的值;
(Ⅱ)若k∈Z,且f(x)+ (3x2﹣5x﹣2k)≥0对任意x∈R恒成立,求k的最大值.
(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(Ⅱ)若直线l经过点(1,0),求直线l被曲线C截得的线段AB的长.