
B .
B . 
C .
C . 
D .
D . 
 B .
B .  D .
D . 



















实验1:将瓶子颈部剪掉,在上端下方1厘米处,打了两个洞,把细线穿进两个洞,打了个结,使它可以悬挂,又在瓶子底部2厘米处面对面穿了两个小孔,把吸管插入,剪去多余部分,露出瓶外2厘米长,并朝着右下方30 度角左右,然后将他悬挂起来,从上往瓶子中倒水,当水浸没小孔,从吸管中流出时,发现瓶子真的跳起来了,并且往顺时针方向转圈(如图),又同样重复了两次,结果都一样。那转圈的速度与什么因素有关呢?他作出了假设,并又进行了下列实验:
实验2:又拿了第二、第三、第四只瓶子,同样在瓶子底部2厘米处分别打3个、4个、6个孔,每孔插入1根吸管,插入的吸管个数分别为3根、4根和6根。重复上述做法,同样每只瓶子做三次,测出运动一周的时间并记录。实验数据记录汇总如下:
| 吸管数 | 第一次时间(s) | 第二次时间(s) | 第三次时间(s) | 平均时间(s) | 瓶子周长(cm) | 运动速度(cm/s) |
| 2 | 6.2 | 6.0 | 6.5 | 6.23 | 20 | 3.21 |
| 3 | 5.1 | 4.7 | 4.9 | 4.9 | 20 | X |
| 4 | 3.8 | 3.7 | 4.0 | 3.83 | 20 | 5.22 |
| 6 | 1.9 | 1.5 | 1.6 | 1.67 | 20 | 11.98 |
回答下列问题:

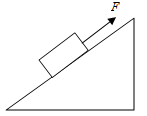
A.可能与物体质量有关;B.可能与斜面倾斜程度有关;C.可能与物体下滑起点的高度有关。
可供选用的器材:质量不同的钢球若干,刻度尺,量筒,秒表。

丙
| 斜面倾斜程度 | 较大 | 较小 | ||||
| 实验次数 | 1 | 2 | 3 | 1 | 2 | 3 |
| 小球从P运动到Q的时间1/s | 5.1 | 5.0 | 5.1 | 5.1 | 5.1 | 5.0 |
【查阅资料】物体从高空下落时,速度越来越大,所受阻力也越来越大,当阻力增大到与重力相等时,将以某一速度作匀速直线运动,这个速度被称为物质下落的收尾速度。
【提出问题】物体从高空下落时的收尾速度与什么有关?
【建立猜想】①可能与物体的体积有关。②可能与物体的有关。
【设计方案】同学们经讨论后认为,可以用小球作为理想化模型来代替生活中的不规则物体作为研究对象进行探究。于是同学们决定取5个不同小的球进行实验,在相同环境条件下,分别从一定高度(足够高)由静止下落,来研究小球从高空下落时的收尾速度与哪些因素有关。
|
小球编号 |
1 |
2 |
3 |
4 |
5 |
|
小球质量m(g) |
2 |
5 |
5 |
5 |
20 |
|
小球半径r(m) |
0.05 |
0.05 |
0.10 |
0.25 |
0.20 |
|
小球收尾速度v(m/s) |
16 |
40 |
10 |
1.6 |
? |
【得出结论】
⑴比较2、3、4号小球的相关实验数据,可以得到的结论是。
⑵根据表中数据,推测5号小球的收尾速度v=m/s
