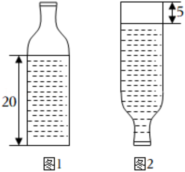
21.
如图①,从大正方体上截去一个小正方体之后,可以得到图②的几何体.
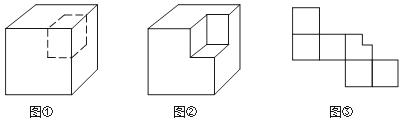
(1)设原大正方体的表面积为S,图②中几何体的表面积为S1 , 那么S1与S的大小关系是
A.S1>S B.S1=S C.S1<S D.无法确定
(2)小明说:“设图①中大正方体各棱的长度之和为l,图②中几何体各棱的长度之和为l1 , 那么l1比l正好多出大正方体3条棱的长度.”你认为这句话对吗?为什么?
(3)如果截去的小正方体的棱长为大正方体棱长的一半,那么图③是图②中几何体的表面展开图吗?如有错误,请予修正.

 B .
B .  D .
D .