山东省潍坊市昌邑市2024届高三上学期数学12月模拟预测试卷

更新时间：2024-03-07 浏览次数：38 类型：高考模拟

一、单项选择题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1. (2023高三上·昌邑模拟) 已知集合A＝{x|y＝lg（3x﹣x²）}，B＝{x|x＜1}，则A∩B＝（）

A . （0，1） B . （﹣∞，0） C . （﹣∞，1） D . [0，1）

答案解析收藏纠错 + 选题
2. (2023高三上·昌邑模拟) 若复数z满足（2+i）z＝5，则在复平面内与复数z对应的点位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2023高三上·昌邑模拟) 已知 $\text{[math]}$ ，条件 $\text{[math]}$ ： $\text{[math]}$ ，条件 $\text{[math]}$ ： $\text{[math]}$ ，则 $\text{[math]}$ 是 $\text{[math]}$ 的（）

A . 充分不必要条件 B . 必要不充分条件 C . 充分必要条件 D . 既不充分也不必要条件

答案解析收藏纠错 + 选题
4. (2023高三上·昌邑模拟) 已知角 $\text{[math]}$ 的终边经过点 $\text{[math]}$ ，则 $\text{[math]}$ （）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
5. (2023高三上·昌邑模拟) 已知a＝log₂3，b＝ln3，c＝ $\text{[math]}$ ，则a ， b ， c的大小关系为（）

A . a＜b＜c B . b＜a＜c C . c＜b＜a D . c＜a＜b

答案解析收藏纠错 + 选题
6. (2023高三上·昌邑模拟) 已知函数y＝f(x)的图象如图所示，则此函数可能是（）

A . f(x)＝ $\text{[math]}$ B . f(x)＝ $\text{[math]}$ C . f(x)＝ $\text{[math]}$ D . f(x)＝ $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023高三上·昌邑模拟) 一个圆锥的轴截面是边长为4的等边三角形，在该圆锥中有一个内接圆柱（下底面在圆锥底面上，上底面的圆周在圆锥侧面上），则当该圆柱侧面积取最大值时，该圆柱的高为（）

A . 1 B . 2 C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023高三上·昌邑模拟) 已知数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则称项 $\text{[math]}$ 为“和谐项”，则数列 $\text{[math]}$ 的所有“和谐项”的平方和为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多项选择题（本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分）

9. (2023高三上·昌邑模拟) 若 $\text{[math]}$ ，则下列不等式中正确的是（）

A . a+b＜ab B . $\text{[math]}$ C . ab＞b² D . a²＞b²

答案解析收藏纠错 + 选题
10. (2023高三上·昌邑模拟) 函数y＝Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）在一个周期内的图象如图所示，则（）

A . 该函数的解析式为 $\text{[math]}$ B . 该函数的对称中心为 $\text{[math]}$ C . 该函数的单调递增区间是 $\text{[math]}$ D . 把函数 $\text{[math]}$ 的图象上所有点的横坐标变为原来的 $\text{[math]}$ ，纵坐标不变，可得到该函数图象

答案解析收藏纠错 + 选题
11. (2023高三上·昌邑模拟) 已知F₁ ， F₂分别是双曲线 $\text{[math]}$ （a＞0，b＞0）的左、右焦点，双曲线左支上存在一点P ，使PF₂²＝8a•PF₁（a为实半轴长）成立，则此双曲线的离心率e的取值可能是（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . 5

答案解析收藏纠错 + 选题
12. (2023高三上·昌邑模拟) 已知函数f（x）＝sinx+x³﹣ax ，则下列结论正确的是（）

A . f（x）是奇函数 B . 若f（x）是增函数，则a≤1 C . 当a＝﹣3时，函数f（x）恰有两个零点 D . 当a＝3时，函数f（x）恰有两个极值点

答案解析收藏纠错 + 选题

三、填空题（本题共4小题，每小题5分，共20分）

13. (2023高三上·昌邑模拟) 已知向量 $\text{[math]}$ ， $\text{[math]}$ 的夹角为60°， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2023高三上·昌邑模拟) 已知点A（﹣2，3）在抛物线C：y²＝2px（p＞0）的准线上，记C的焦点为F ，则直线AF的斜率为．

答案解析收藏纠错 + 选题
15. (2023高三上·昌邑模拟) 地面上有并排的七个汽车位，现有红、白、黄、黑四辆不同的汽车同时倒车入库，当停车完毕后，恰有两个连续的空车位，且红、白两车互不相邻的情况有种．

答案解析收藏纠错 + 选题
16. (2023高三上·昌邑模拟) 在棱长为2的正方体ABCD﹣A₁B₁C₁D₁中，M ， N ， Q分别为棱A₁B₁ ， B₁C₁ ， BB₁的中点，点P为棱CC₁上的动点，则V_P_﹣_MNQ的最大值为，若点P为棱CC₁的中点，三棱锥M﹣PQN的顶点在同一个球面上，则该球的表面积为．

答案解析收藏纠错 + 选题

四、解答题（本题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤）

17. (2023高三上·昌邑模拟) 已知公差不为零的等差数列{a_n}的前四项和为10，且a₂ ， a₃ ， a₇成等比数列．
1. （1）求数列{a_n}通项公式；
2. （2）设 $\text{[math]}$ ，求数列{b_n}的前n项和S_n ．
答案解析收藏纠错 + 选题
18. (2023高三上·昌邑模拟) 在△ABC中，c＝1， $\text{[math]}$ ，且△ABC的面积为 $\text{[math]}$ ．
1. （1）求a的值；
2. （2）若D为BC上一点，且 ▲ ，求sin∠ADB的值．
  从①AD＝1，② $\text{[math]}$ 这两个条件中任选一个，补充在上面问题中并作答．
答案解析收藏纠错 + 选题
19. (2023高三上·昌邑模拟) 如图，在矩形ABCD中，AB＝2AD ，点E是CD的中点．将△ADE沿AE折起，使得点D到达点P的位置，且使平面PAE⊥平面ABCE ．
1. （1）求证：平面PBE⊥平面PAE；
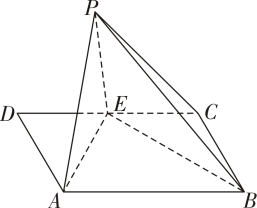
2. （2）求平面PAE与平面BCP所成锐二面角的余弦值．
答案解析收藏纠错 + 选题
20. (2023高三上·昌邑模拟) 心理学家发现视觉和空间能力与性别有关，某数学兴趣小组为了验证这个结论，从兴趣小组中按分层抽样的方法抽取50名同学（男30名女20名），给所有同学几何题和代数题各一题，让各位同学自由选择一道题进行解答，选题情况如表：（单位：人）

几何题
代数题
总计
男同学
22
8
30
女同学
8
12
20
总计
30
20
50
1. （1）能否据此判断有97.5%的把握认为视觉和空间能力与性别有关？
2. （2）现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究，记甲、乙两名女生被抽到的人数为X ，求X的分布列及数学期望E（X）．
  附表及公式
  P（k²≥k）
  0.15
  0.10
  0.05
  0.025
  0.010
  0.005
  0.001
  k
  2.072
  2.706
  3.841
  5.024
  6.635
  7.879
  10.828
  $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2023高三上·昌邑模拟) 已知椭圆C： $\text{[math]}$ （a＞b＞0）的长轴长为4，且点（1，e）在椭圆C上，其中e是椭圆C的离心率．
1. （1）求椭圆C的方程；
2. （2）若斜率为 $\text{[math]}$ 的直线l与椭圆C交于M、N两点，且点M在第一象限，点A、B分别为椭圆C的右顶点和上顶点，求四边形AMBN面积S的最大值．
答案解析收藏纠错 + 选题
22. (2023高三上·昌邑模拟) 已知函数f（x）＝2xe^x﹣a（x+lnx）（a∈R）．
1. （1）若a＝1，求y＝f（x）在（1，f（1））处的切线方程；
2. （2）若x₀是函数f（x）的极值点，且f（x₀）＞0，求证：f（x）＞4x₀﹣4x₀³ ．
答案解析收藏纠错 + 选题