湖南省株洲市部分中学2023-2024年高一上学期期末考试数...

更新时间：2024-04-17 浏览次数：20 类型：期末考试

一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. (2024高一上·株洲期末) 已知命题 $\text{[math]}$ ，则p的否定为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高一上·株洲期末) 集合 $\text{[math]}$ 的子集个数为（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
3. (2024高一上·株洲期末) 下列大小关系错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高一上·株洲期末) 已知函数 $\text{[math]}$ 的定义域为D，区间 $\text{[math]}$ ，设 $\text{[math]}$ ，其中 $\text{[math]}$ ，则“ $\text{[math]}$ $\text{[math]}$ ”是“函数 $\text{[math]}$ 在区间I上单调递增”的（）

A . 充分必要条件 B . 必要不充分条件 C . 充分不必要条件 D . 既不充分也不必要条件

答案解析收藏纠错 + 选题
5. (2024高一上·株洲期末) 已知函数 $\text{[math]}$ ，现用二分法求函数 $\text{[math]}$ 在 $\text{[math]}$ 内的零点的近似值，则使用两次二分法后，零点所在区间为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024高一上·株洲期末) 从A地到B地的距离约为 $\text{[math]}$ ，经多次实验得到一辆汽车每小时耗油量Q（单位：L）与速度v（单位：km/h）（ $\text{[math]}$ ）的如下数据：
v
0
40
60
80
120
Q
0
7
8
10
20
为了描述汽车每小时耗油量Q与速度v的关系，下列最符合实际的函数模型是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高一上·株洲期末) 已知 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高一上·株洲期末) 已知函数 $\text{[math]}$ 对 $\text{[math]}$ ，都有 $\text{[math]}$ ，若 $\text{[math]}$ 在 $\text{[math]}$ 上存在最大值M和最小值m，则 $\text{[math]}$ （）

A . 8 B . 4 C . 2 D . 0

答案解析收藏纠错 + 选题

二、多选题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9. (2024高一上·株洲期末) 已知集合M，N满足 $\text{[math]}$ ，则集合M，N可能是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高一上·株洲期末) 已知函数 $\text{[math]}$ ，则（）

A . $\text{[math]}$ 的定义域为 $\text{[math]}$ B . $\text{[math]}$ 的值域为R C . $\text{[math]}$ 为增函数 D . $\text{[math]}$ 的图象关于坐标原点对称

答案解析收藏纠错 + 选题
11. (2024高一上·株洲期末) 已知正数m ， n满足 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2024高一上·株洲期末) 已知函数 $\text{[math]}$ ，将 $\text{[math]}$ 图象上的所有点向左平移 $\text{[math]}$ 个单位，得到函数 $\text{[math]}$ 的图象，则下列结论正确的有（）

A . $\text{[math]}$ B . 函数 $\text{[math]}$ 的单调递减区间为 $\text{[math]}$ C . 若存在 $\text{[math]}$ 使得 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值与最小值的和为 $\text{[math]}$ D . 设直线 $\text{[math]}$ 与 $\text{[math]}$ 和 $\text{[math]}$ 的图象分别交于M，N两点，则 $\text{[math]}$ 的最大值为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共4小题，每小题5分，共20分．

13. (2024高一上·株洲期末) 已知角 $\text{[math]}$ 的终边经过点 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024高一上·株洲期末) 某汽车租赁公司的月收益y（单位：千元）与每辆车的月租金x（单位：千元）间的关系为 $\text{[math]}$ ．若要使公司的月收益最大，则每辆车的租金为千元．

答案解析收藏纠错 + 选题
15. (2024高一上·株洲期末) 函数 $\text{[math]}$ （其中 $\text{[math]}$ …为自然对数的底数）的反函数为 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2024高一上·株洲期末) 若函数 $\text{[math]}$ 在 $\text{[math]}$ 上的最大值为2，则实数 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

四、解答题：本题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤

17. (2024高一上·株洲期末) 求下列各式的值：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2024高一上·株洲期末) 已知函数 $\text{[math]}$ ．
1. （1）若函数 $\text{[math]}$ 为偶函数，求实数m的值；
2. （2）若函数 $\text{[math]}$ 的定义域为R，求实数m的取值范围．
答案解析收藏纠错 + 选题
19. (2024高一上·株洲期末) 已知函数 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的定义域与最小正周期；
2. （2）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值域
答案解析收藏纠错 + 选题
20. (2024高一上·株洲期末) 为了响应国家“土地流转”政策，某公司在城郊租赁了大量土地作为蔬菜种植基地，种植的蔬菜销往城内各大超市和农贸市场．今年冬季的某一天（记为第1天）有一批绿色有机大白菜开始陆续上市．据预测，大白菜上市的第1天至第60天内，每天的产量x（单位：kg）（注：每天的产量即为每天的销售量）近似地满足图1所示的两条线段对应的函数关系；每天的销售价格y（单位：元/kg）近似地满足图2（其中前一段为线段，后一段为函数 $\text{[math]}$ ） $\text{[math]}$ 所示的函数关系．
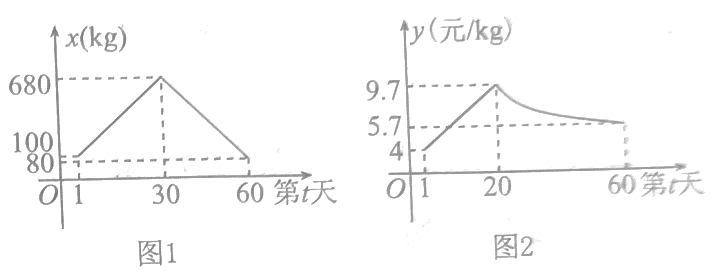
1. （1）求这60天内每天的产量x，每天的销售价格y与第t天的函数关系；
2. （2）从开始销售起第几天的销售收入w（单位：元）最大?最大的销售收入是多少元?
答案解析收藏纠错 + 选题
21. (2024高一上·株洲期末) 已知 $\text{[math]}$ 为二次函数， $\text{[math]}$ ，不等式 $\text{[math]}$ 的解集为 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的解析式；
2. （2）若函数 $\text{[math]}$ 在 $\text{[math]}$ 上的值域为 $\text{[math]}$ ，求s，t满足的条件．
答案解析收藏纠错 + 选题
22. (2024高一上·株洲期末) 已知函数 $\text{[math]}$ 在定义域 $\text{[math]}$ 上为减函数，且值域为 $\text{[math]}$
1. （1）证明： $\text{[math]}$ ；
2. （2）求实数m的取值范围；
3. （3）求 $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题