浙江省宁波市十二校联考2024-2025学年七年级上学期数学...

更新时间：2024-11-20 浏览次数：1 类型：期中考试

一、 选择题 (每小题 3 分, 共 30 分

1. (2024七上·南山期中) 2024的相反数是（　　）

A . 2024 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024七上·宁波期中) 已知下列各数： $\text{[math]}$ ，其中负有理数有 ( )

A . 1 个 B . 2 个 C . 3 个 D . 4 个

答案解析收藏纠错 + 选题
3. (2024七上·宁波期中) 宁波市商务局发布的统计数据显示， 2024 年 10 月 1 日至 7 日，全市重点监测的 50 家零售、餐饮企业累计实现销售额 915000000 元，较去年同期略有增长。将数据 915000000 用科学记数法表示应为 ( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七上·宁波期中) 下列说法中正确的个数是 ( )
① 0 是绝对值最小的有理数 ②相反数大于本身的数是负数 ③一个有理数不是整数就是分数 ④一个有理数不是正数就是负数 ⑤无理数都可以用数轴上的点来表示 ⑥一个数的立方根有两个，它们互为相反数

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
5. (2024七上·宁波期中) 用2，0，2，4这四个数进行如下运算，计算结果最大的式子是 ( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024七上·宁波期中) 面积为15的正方形的边长为m，则m的值在（）

A . 1和2之间 B . 2和3之间 C . 3和4之间 D . 4和5之间

答案解析收藏纠错 + 选题
7. (2024七上·宁波期中) 用 $\text{[math]}$ 表示的数一定是 ( )

A . 正数 B . 负数 C . 正数或负数 D . 都不对

答案解析收藏纠错 + 选题
8. (2024七上·宁波期中) 一台电视机成本价为 $\text{[math]}$ 元，销售价比成本价增加了 $\text{[math]}$ ，因库存积压，所以就按销售价的 $\text{[math]}$ 出售，那么每台实际售价为 ( )

A . $\text{[math]}$ 元 B . $\text{[math]}$ 元 C . $\text{[math]}$ 元 D . $\text{[math]}$ 元

答案解析收藏纠错 + 选题
9. (2024七上·宁波期中) 实数a，b，c在数轴上的对应点的位置如图所示，若|a|=|b|，则下列结论中错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024七上·宁波期中) 如图，7张全等的小长方形纸片(既不重叠也无空隙)放置于矩形ABCD中，设小长方形的长为a，宽为b(a>b)，若要求出两块黑色阴影部分的周长和，则只要测出下面哪个数据（）

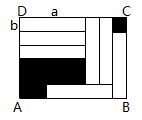
A . a B . b C . a+b D . a-b

答案解析收藏纠错 + 选题

二、 填空题 (每小题 3 分, 共 24 分

11. (2024七上·宁波期中) 如果温度上升 $\text{[math]}$ ，记作 $\text{[math]}$ ，那么温度下降 $\text{[math]}$ 记作 ℃ .

答案解析收藏纠错 + 选题
12. (2024七上·宁波期中) 计算： $\text{[math]}$ ， $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2024七上·宁波期中) 写出两个无理数，使它们的和为有理数，它们可以是.

答案解析收藏纠错 + 选题
14. (2024七上·宁波期中) 近似数 $\text{[math]}$ ，精确到位．

答案解析收藏纠错 + 选题
15. (2024七上·宁波期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ =.

答案解析收藏纠错 + 选题
16. (2024七上·宁波期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
17. (2024七上·宁波期中) 已知 $\text{[math]}$ 和 $\text{[math]}$ 都是正数 $\text{[math]}$ 的平方根，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
18. (2024七上·宁波期中) 已知 $\text{[math]}$ 表示 4 个不同的正整数，满足 $\text{[math]}$ ，其中 $\text{[math]}$ ，则
$\text{[math]}$ 的最大值是.

答案解析收藏纠错 + 选题

三、解答题 (19 题 10 分, 20 题 7 分, 21 题 8 分, 22 题 11 分, 23 题 10 分, 共 46 分

19. (2024七上·宁波期中) 计算：
1. （1） . $\text{[math]}$
2. （2） . $\text{[math]}$
3. （3） $\text{[math]}$
4. （4） . $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2024七上·宁波期中) 某水果店以每箱90元的价格从水果批发市场购进20箱樱桃，若以每箱净重5千克为标准，超过的千克数记为正数，不足的千克数记为负数，称重的记录如表：
与标准重量的差值(单位：千克)
-0.5
-0.25
0
0.2
0.25
0.5
箱数
2
2
4
5
n
3
1. （1）求 $\text{[math]}$ 的值及这20箱樱桃的总重量；
2. （2）该水果店第一天以每千克25元的价格销售了这批樱桃的70%，第二天因为害怕剩余樱桃腐烂，决定降价把剩余的樱桃以第一天零售价的60%全部售出．水果店在销售这批樱桃过程中是盈利还是亏损，盈利或亏损多少元?
答案解析收藏纠错 + 选题
21. (2024七上·宁波期中) 初中阶段，目前我们已经学习了多种计算技巧，例如裂项相消法、错位相减法等，请计算下列各式：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ；
3. （3） $\text{[math]}$ ；
4. （4） $\text{[math]}$ .
答案解析收藏纠错 + 选题
22. (2024七上·宁波期中) 结合数轴与绝对值的知识，回答下列问题：
1. （1）数轴上表示 4 和 1 的两点之间的距离是；表示 -3 和 2 的两点之间的距离是；一般地，数轴上表示数 $\text{[math]}$ 和 $\text{[math]}$ 的两点之间的距离等于 $\text{[math]}$ ，数轴上表示 $\text{[math]}$ 和 -1 的两点之间的距离是；如果表示数 $\text{[math]}$ 和 -2 的两点之间的距离是 3，那么 $\text{[math]}$ .
2. （2）若数轴上表示 $\text{[math]}$ 的点位于 -5 和 3 之间，求 $\text{[math]}$ 的值.
3. （3）当 $\text{[math]}$ 为时， $\text{[math]}$ 最小，最小值为.
4. （4）若 $\text{[math]}$ ，请直接写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
23. (2024七上·宁波期中) 如图，数轴上有 $\text{[math]}$ 两点， $\text{[math]}$ 之间距离为 21，原点 $\text{[math]}$ 在 $\text{[math]}$ 之间， $\text{[math]}$ 到 $\text{[math]}$ 的距离是 $\text{[math]}$ 到 $\text{[math]}$ 的距离的两倍.
1. （1）点 $\text{[math]}$ 表示的数为，点 $\text{[math]}$ 表示的数为；
2. （2）点 $\text{[math]}$ 、点 $\text{[math]}$ 和点 $\text{[math]}$ (点 $\text{[math]}$ 初始位置在原点 $\text{[math]}$ ) 同时向左运动，它们的速度分别为 1 ， 2，2 个单位长度每秒，则经过多少秒，点 $\text{[math]}$ 到点 $\text{[math]}$ 与点 $\text{[math]}$ 的距离相等?
3. （3）点 $\text{[math]}$ 沿着数轴移动，每次只允许移动 1 个单位长度，经过 8 次移动后，点 $\text{[math]}$ 与原点 $\text{[math]}$ 相距 1 个单位长度. 满足条件的点 $\text{[math]}$ 的移动方法共有多少种?
4. （4）点 $\text{[math]}$ 和点 $\text{[math]}$ 同时沿着数轴移动，两点每次均只允许移动 1 个单位长度. 请判断点 $\text{[math]}$ 和点 $\text{[math]}$ 经过相同次数的移动后，能否同时到达原点 $\text{[math]}$ ? 如果能，请给出点 $\text{[math]}$ 和点 $\text{[math]}$ 各自的移动方法；如果不能，请说明理由.
答案解析收藏纠错 + 选题