1. (2019·大同模拟) 阅读下列材料，并完成相应的任务．

托勒密定理：

托勒密（Ptolemy）（公元90年～公元168年），希腊著名的天文学家，他的要著作《天文学大成》被后人称为“伟大的数学书”，托勒密有时把它叫作《数学文集》，托勒密从书中摘出并加以完善，得到了著名的托勒密（Ptolemy）定理．

托勒密定理：

圆内接四边形中，两条对角线的乘积等于两组对边乘积之和．

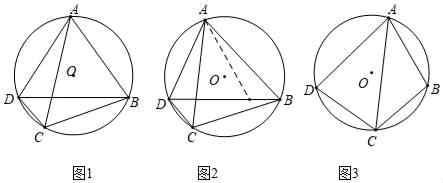
已知：如图1，四边形ABCD内接于⊙O，

求证：AB•CD+BC•AD＝AC•BD

下面是该结论的证明过程：

证明：如图2，作∠BAE＝∠CAD，交BD于点E．

∵

∴∠ABE＝∠ACD

∴△ABE∽△ACD

∴

∴AB•CD＝AC•BE

∵

∴∠ACB＝∠ADE（依据1）

∵∠BAE＝∠CAD

∴∠BAE+∠EAC＝∠CAD+∠EAC

即∠BAC＝∠EAD

∴△ABC∽△AED（依据2）

∴AD•BC＝AC•ED

∴AB•CD+AD•BC＝AC•（BE+ED）

∴AB•CD+AD•BC＝AC•BD

任务：

1. （1） 上述证明过程中的“依据1”、“依据2”分别是指什么？
3. （2） 当圆内接四边形ABCD是矩形时，托勒密定理就是我们非常熟知的一个定理：．

   （请写出）

5. （3） 如图3，四边形ABCD内接于⊙O，AB＝3，AD＝5，∠BAD＝60°，点C为 的中点，求AC的长．