1. (2019八下·太原期中) 综合与实践：

问题情境：

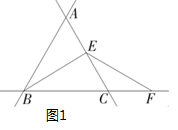
在数学综合与实践课上，张老师启示大家利用直线、线段以及点的运动变换进行探究活动.变换条件如下：如图1，直线AB，AC，BC两两相交于A，B，C三点，得知△ABC是等边三角形，点E是直线AC上一动点（点E不与点A，C重合），点F在直线BC上，连接BE，EF，使EF=BE．

独立思考：

1. （1） 张老师首先提出了这样一个问题：如图1，当E是线段AC的中点时，确定线段AE与CF的数量关系，请你直接写出结论：AECF（填“＞”“＜”或“=”）.

   提出问题：

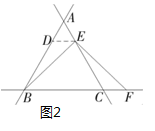
3. （2） “奋斗”小组受此问题的启发，提出问题：若点E是线段AC上的任意一点，其他条件不变，（1）中的结论是否成立？该小组认为结论仍然成立，理由如下：如图2，过点E作ED∥BC，交AB于点D．（请你补充完整证明过程）
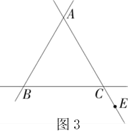
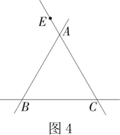
5. （3） “缜密”小组提出的问题是：动点E的运动位置如图3，图4所示，其他条件不变，根据题意补全图形，并判断线段AE与CF的数量关系是否发生变化？请你选择其中一种予以证明.

   

7. （4） “爱心”小组提出的问题是：若等边△ABC的边长为 ，AE=1，则BF的长为.（请你直接写出结果）．