1. (2020七下·杭州期中) 已知D是△ABC的BC边上一点，连结AD，此时有结论 ，请解答下列问题：

1. （1） 当D是BC边上的中点时，△ABD的面积 △ACD的面积(填“>”“<”或“=”)。
3. （2） 如图1，点D、E分别为AB，AC边上的点，连结CD，BE交于点O，若△BOD、△COE、△BOC的面积分别为5，8，10，则△ADE的面积是(直接写出结论)。
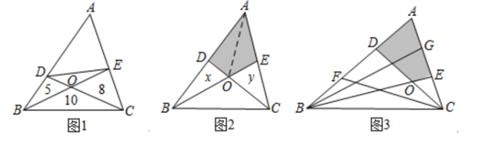
5. （3） 如图2，若点D，E分别是△ABC的AB，AC边上的中点，且S_△ABC=60，求四边形ADOE的面积。可以用如下方法：连结AO，由AD=DB得S_△ADO=S_△BDO ， 同理：S_△CEO=S_△AEO ， 设S_△BDO=x，S_△CEO=y，则S_△ADO=x，S_△AEO=y，由题意得S_△ABE= S_△ABC=30，S_△ADC= S_△ABC=30，可列方程组为 ，解得x+y=20，可得四边形ADOE的面积为20。解答下面问题：

   如图3，D，F是AB的三等分点，E，G是CA的三等分点，CD与BE交于O，且S_△ABC=60，请计算四边形ADOE的面积，并说明理由。