问题背景:
如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.
小吴同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90°到△AED处,点B,C分别落在点A,E处(如图②),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=  CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=  CD.
CD.
简单应用:
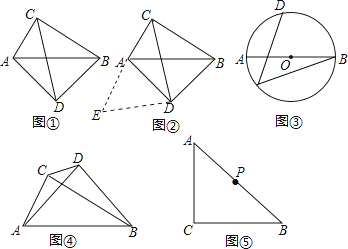
-
(1)
在图①中,若AC=

,BC=2

,则CD=
.
-
-
(2)
如图③,AB是⊙O的直径,点C、D在⊙上,

=

,若AB=13,BC=12,求CD的长.
拓展规律:
-
-
(3)
如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的长(用含m,n的代数式表示)
-
-
(4)
如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE=

AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是
.
-
CD,从而得出结论:AC+BC=
CD.
