1. (2020九下·滨湖月考) 数学学习小组“陆月辉煌”最近正在进行几何图形组合问题的研究.认真研读以下四个片段，并回答问题.

1. （1） 小陆说：将一块足够大的等腰直角三角板置于一个正方形中，直角顶点与对角线交点O重合，在转动三角板的过程中我发现某些线段之间存在确定的数量关系.

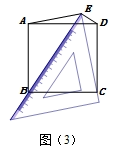
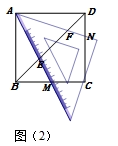
   如图（1），若三角板两条直角边的外沿分别交正方形的边AB、BC于点M、N，则①OM＋ON=MB＋NB；② .

   请你判断他的猜想是否正确？并证明你认为正确的猜想.

   

3. （2） 小月说：将三角板中一个45°角的顶点和正方形的一个顶点重合放置，使得这个角的两条边与正方形的一组邻边有交点.

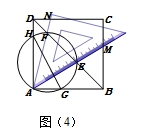
   如图（2），若以A为顶点的45°角的两边分别交正方形的边BC、CD于点M、N，交对角线BD于点E、F.我发现：BE²＋DE²=2AE² ， 只要准确旋转图（2）中的一个三角形就能证明这个结论.

   请你写出小月所说的具体的旋转方式：.

   

5. （3） 小辉说：将三角板的一个45°角放置在正方形的外部，同时角的两边恰好经过正方形两个相邻的顶点.

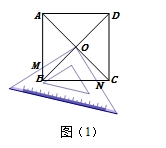
   如图（3），设顶点为E的45°角位于正方形的边AD上方，这个角的两边分别经过点B、C，连接EA，ED.那么线段EB、EC、ED也存在确定的数量关系：（EB＋ED）²=2EC².

   请你证明这个结论.

   

7. （4） 小煌说：在图（2）中，作一个过点A、E、F的圆，交正方形的边AB、AD于点G、H，如图（4）所示.你知道线段DH、HG、GB三者之间的关系吗？请直接写出结论：.