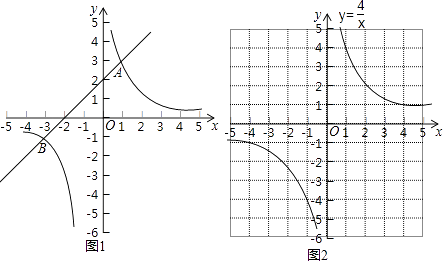
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= 交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2 , 即通过观察函数的图象,可以得到不等式ax+b> 的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.
下面是他的探究过程,请将探究过程补充完整:
将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1> ;
当x<0时,原不等式可以转化为x2+4x﹣1< ;
设y3=x2+4x﹣1,y4= ,在同一坐标系中分别画出这两个函数的图象.
双曲线y4= 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为;
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为.