1. (2019九上·永定期中) 如图

1. （1） 如图1，点P是等边△ABC内一点，已知PA＝3，PB＝4，PC＝5，求∠APB的度数．

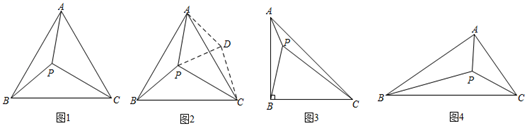
   分析：要直接求∠A的度数显然很因难，注意到条件中的三边长恰好是一组勾股数，因此考虑借助旋转把这三边集中到一个三角形内．

   解：如图2，作∠PAD＝60°使AD＝AP，连接PD，CD，则△PAD是等边三角形．

   ∴＝AD＝AP＝3，∠ADP＝∠PAD＝60°

   ∵△ABC是等边三角形

   ∴AC＝AB，∠BAC＝60°∴∠BAP＝

   ∴△ABP≌△ACD

   ∴BP＝CD＝4，＝∠ADC

   ∵在△PCD中，PD＝3，PC＝5，CD＝4，PD²+CD²＝PC²

   ∴∠PDC＝°

   ∴∠APB＝∠ADC＝∠ADP+∠PDC＝60°+90°＝150°

3. （2） 如图3，在△ABC中，AB＝BC，∠ABC＝90°，点P是△ABC内一点，PA＝1，PB＝2，PC＝3，求∠APB的度数．
5. （3） 拓展应用．如图4，△ABC中，∠ABC＝30°，AB＝4，BC＝5，P是△ABC内部的任意一点，连接PA，PB，PC，则PA+PB+PC的最小值为．