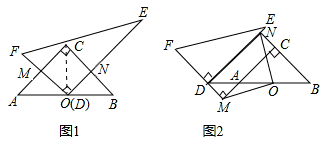
1. (2020八上·科尔沁期末) 问题情境：将一副直角三角板（Rt△ABC和Rt△DEF）按图1所示的方式摆放，其中∠ACB=90°，CA=CB，∠FDE=90°，O是AB的中点，点D与点O重合，DF⊥AC于点M，DE⊥BC于点N，试判断线段OM与ON的数量关系，并说明理由．

探究展示：小宇同学展示出如下正确的解法：

解：OM=ON，证明如下：

连接CO，则CO是AB边上中线，

∵CA=CB，∴CO是∠ACB的角平分线．（依据1）

∵OM⊥AC，ON⊥BC，∴OM=ON．（依据2）

反思交流：

1. （1） 上述证明过程中的“依据1”和“依据2”分别是指：

   依据1：

   依据2：

3. （2） 你有与小宇不同的思考方法吗？请写出你的证明过程．

   拓展延伸：

5. （3） 将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置，使点D落在BA的延长线上，FD的延长线与CA的延长线垂直相交于点M，BC的延长线与DE垂直相交于点N，连接OM、ON，试判断线段OM、ON的数量关系与位置关系，并写出证明过程．