1. (2017·黄冈模拟)

如图，在平面直角坐标系中，矩形OABC的边OA=2，OC=6，在OC上取点D将△AOD沿AD翻折，使O点落在AB边上的E点处，将一个足够大的直角三角板的顶点P从D点出发沿线段DA→AB移动，且一直角边始终经过点D，另一直角边所在直线与直线DE，BC分别交于点M，N．

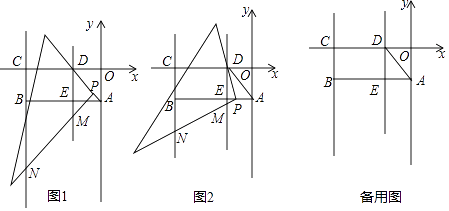
1. （1） 填空：经过A，B，D三点的抛物线的解析式是；

3. （2） 已知点F在（1）中的抛物线的对称轴上，求点F到点B，D的距离之差的最大值；

5. （3） 如图1，当点P在线段DA上移动时，是否存在这样的点M，使△CMN为等腰三角形？若存在，请求出M点坐标；若不存在，请说明理由；

7. （4） 如图2，当点P在线段AB上移动时，设P点坐标为（x，﹣2），记△DBN的面积为S，请直接写出S与x之间的函数关系式，并求出S随x增大而增大时所对应的自变量x的取值范围．