1. (2021·九台模拟) （教材呈现）下面是华师版八年级下册教材第89页的部分内容．

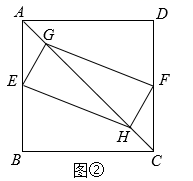
如图，G ， H是平行四边形ABCD对角线AC上的两点，且AG=CH ， E ， F分别是边AB和CD的中点

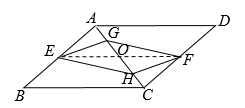
求证：四边形EHFG是平行四边形

证明：连接EF交AC于点O

∵四边形ABCD是平行四边形

∴AB=CD ， AB∥CD

又∵E ， F分别是AB ， CD的中点

∴AE=CF

又∵AB∥CD

∴∠EAO=∠FCO

又∵∠AOE=∠COF

∴△AOE≌△COF

1. （1） 请补全上述问题的证明过程．
3. （2）

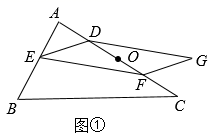
   （探究）如图①，在△ABC中，E，O分别是边AB、AC的中点，D、F分别是线段AO、CO的中点，连结DE、EF，将△DEF绕点O旋转180°得到△DGF，若四边形DEFG的面积为8，则△ABC的面积为．

   

    

5. （3） （拓展）如图②，GH是正方形ABCD对角线AC上的两点，且AG＝CH ， GH＝AB ， E、F分别是AB和CD的中点．若正方形ABCD的面积为16，则四边形EHFG的面积为．