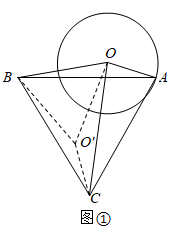

解:将线段OB绕点B顺时针旋转60°到O′B,连接OO′,CO′.
由旋转的性质知:∠OBO′=60°,BO′=BO=6,即△OBO′是等边三角形.
∴OO′=BO=6
又∵△ABC是等边三角形
∴∠ABC=60°,AB=BC
∴∠OBO′=∠ABC=60°
∴∠OBA=∠O′BC
在△OBA和△O′BC中,
∴(SAS)
∴OA=O′C
在△OO′C中,OC<OO′+O′C
当O,O′,C三点共线,且点C在OO′的延长线上时,OC=OO′+O′C
即OC≤OO′+O′C
∴当O,O′,C三点共线,且点C在OO′的延长线上时,OC取最大值,最大值是 .