1.
(2021七下·花都期末)
“长度”和“角度”是几何学研究的核心问题.相交线与平行线的学习,让我们对“角度转化”有了深刻的体会.某数学兴趣小组受此启发,试图沟通“角度”与“长度”间的关系.在研究过程中他们发现了一条关于三角形的重要结论----“等角对等边”,即:如果一个三角形有两个角相等,那么这两个角所对的边也相等.
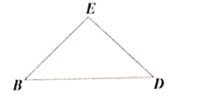
如右图,在  中,若
中,若  ,则
,则  .
.
以此为基础,该兴趣小组邀请你加入研究,继续解决如下新问题:
在平面直角坐标系中,  ,
,  ,已知
,已知  ,点
,点  为
为  轴上方的一点.
轴上方的一点.
-
(1)
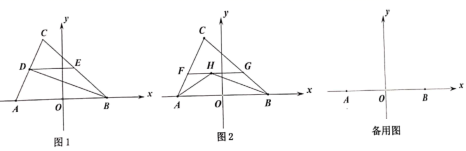
如图1,若

的角平分线交

于点

,已知点

,

上有一点

.则①

与

轴的位置关系为
▲ ;②求

的长度;
-
-
(2)
如图2,

、

分别平分

、

,过

点作

的平行线,分别交

、

于点

、

.若

,

,求四边形

的周长;
-
-
(3)
当点

为

轴上方的一动点(不在

轴上)时,连接

、

.若

邻补角的角平分线和

的角平分线交于点

,过点

作

的平行线,分别交
直线 
、
直线 
于点

、

.随着点

移动,图形形状及点

、

、

的位置也跟着变化,但线段

、

和

之间却总是存在着确定的数量关系,请直接写出这三条线段之间的数量关系
.
-

中,若
,则
.
,
,已知
,点
为
轴上方的一点.
