角平分线回忆
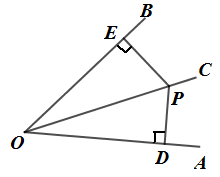
我们已经知道角是轴对称图,角平分线所在的直线是角的对称轴,如图, 是
的角平分线,F是
上的任意一点,作
,
,垂足分别为点D和点E,将
沿
对折,我们发现
与
完全重合,由此即有角平分线的性质定理:角平分线上的点到角两边的距相等.
已知:如图, 是
的平分线,点P是
上的任意一点,
,
,垂直分别为D和点E.
求证: .
请写出定理的证明过程
分析:图中有两个直角三角形 和
只要证明这两个三角形全等,即可证明
.
请根据教材中的分折,结合图①,写出“角平分线的性质定理”完整的证明过珵.
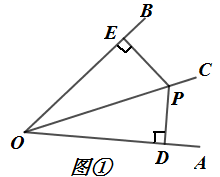
证明:∵ 是
的平分线,
∴ ,
∵ ,
∴ ,
在 和
中,
,
∴ ,
∴
如图②,在四边形 中,
,点E在边
上,
平分
,
平分
.
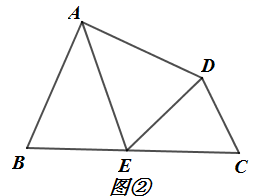
求证: .