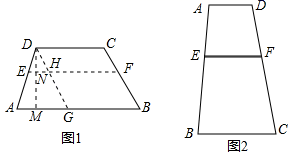
如图1,四边形ABCD中,AB∥CD,AB=a,CD=b(a≠b),点E、F分别是AD、BC上的点,且EF∥AB,设EF到CD、AB的距离分别为d1、d2 .
[初步尝试]
小亮同学在对这一图形进行研究时,发现如下事实:
⑴当 时,有EF=
;
⑵当 时,有EF=
.
该同学思考研究(2)的过程如下:
作DG∥BC,交AB于G,作DM⊥AB于点M,交EF于点N.
显然HF=CD=b,AG=AB﹣CD=a﹣b.
易证,△DEH∽△DAG,可得 =
,
即, =
而由 ,得
=
,
代入上式,则 =
.
解得EH= (a﹣b)
∴EF=EH+HF=b+ (a﹣b)=
[类比发现]
沿用上述图形和已知条件,请自主完成进一步的研究发现:
当 时,EF=;
当 时,EF=;
当 时,EF=;
当 时,EF=.(其中m、n均为正整数,下同)
[推广证明]
当 时,EF=;
请证明你的结论.
[实际应用]
请结合所给情景,创设一个需要采用下面的全部信息求解的问题.
[情景]
如图2,有一块四边形耕地ABCD,AD∥BC,AD=100米,BC=300米,AB=500米,在AB上取点E,使AE=200米,以点E处为起点开挖平行于两底的水渠EF,与CD边相交于点F.
[问题]
?(提问即可,不必求解)