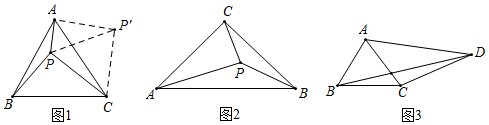
利用旋转变换解决数学问题是一种常用的方法.如图1,点P是等边三角形ABC内一点,PA=1,PB= , PC=2.求∠BPC的度数.
为利用已知条件,不妨把△BPC绕点C顺时针旋转60°得△AP′C,连接PP′,则PP′的长为;在△PAP′中,易证∠PAP′=90°,且∠PP′A的度数为,综上可得∠BPC的度数为;
如图2,点P是等腰Rt△ABC内的一点,∠ACB=90°,PA=2,PB= , PC=1,求∠APC的度数;
如图3,在四边形ABCD中,BC=3,CD=5,AB=AC=AD.∠BAC=2∠ADC,请直接写出BD的长.