1. (2021八下·崂山期中) 阅读理解并解答：

1. （1） 我们把多项式a²+2ab+b²及a²﹣2ab+b²叫做完全平方式在运用完全平方公式行因式分解时，关键是判断这个多项式是不是一个完全平方式，同样地，把一个多项式进行部分因式分解可以解决代数式的值的最大（或最小）值问题．

   例如：①x²+2x+3＝（x²+2x+1）+2＝（x+1）²+2，

   ∵（x+1）²是非负数，即（x+1）²≥0， 

   ∴（x+1）²+2≥2．则这个代数式x²+2x+3的最小值是，这时相应的x的值是．

   ②3x²﹣12x+5＝3（x²﹣4x）+5＝3（x²﹣4x+4﹣4）+5＝3（x﹣2）²﹣12+5＝3（x﹣2）²﹣7，

   ∵（x﹣2）²是非负数，即（x﹣2）²≥0，

   ∴3（x﹣2）²﹣7≥﹣7．

   则这个代数式3x²﹣12x+5的最小值是，这时相应的x的值是．

3. （2） 仿照上述方法求代数式﹣x²﹣14x+10的最大或最小值，并写出相应的x的值；
5. （3） 实践应用：如图，工人师傅要在等腰直角△AEF的内部作一个矩形ABCD（矩形对边相等），其中AB和AD分别在两直角边上，  ，∠DCB＝90°．

   

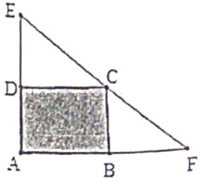
   ①如果设矩形的一边AB＝xcm，那么AD边的长度为　      　cm；

   ②请用含x的代数式表示矩形ABCD的面积，求出当x取何值时，矩形ABCD的面积最大，最大值是多少？