1. (2022·淄川模拟)              

1. （1） 【问题发现】

   

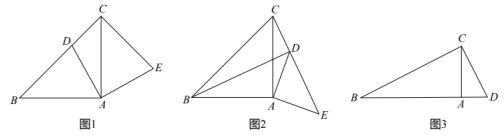
   如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D为斜边BC上一点（不与点B，C重合），将线段AD绕点A顺时针旋转90°得到AE，连接EC，则线段BD与CE的数量关系是，位置关系是；

3. （2） 【探究证明】

   如图2，在Rt△ABC和Rt△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，将△ADE绕点A旋转，当点C，D，E在同一条直线上时，BD与CE具有怎样的位置关系，说明理由；

5. （3） 【拓展延伸】

   如图3，在Rt△BCD中，∠BCD＝90°，BC＝2CD＝4，过点C作CA⊥BD于A．将△ACD绕点A顺时针旋转，点C的对应点为点E．设旋转角∠CAE为（0°＜＜360°），当C，D，E在同一条直线上时，画出图形，并求出线段BE的长度．