分析:在数学运算表达式中,运算符总是置于与之相关的两个运算对象之间,在计算结果时,要考虑括号、运算符号的优先性。为了程序实现的方便,波兰逻辑学家J.Lukasiewicz提出了另一种表示法,将运算符置于其运算对象之后,没有括号,不用考虑运算符号的优先性。这种表达式称为后缀表达式,又叫逆波兰表达式。
如表达式“682-2*3÷+”是四则运算式“6+(8-2)*2÷3”的逆波兰表达式。为了处理方便, 规定表达式中的数均为小于 10 的正整数, 运算符为+ - * ÷。
⑴抽象建模
设计两个栈bds、fh,栈bds用来存放表达式,栈fh用来暂时存放运算符。从左往右扫描四则运算式,遇到数字时,入栈bds;遇到运算符号时,根据运算符号的优先级设计进栈与出栈。
四则运算式“6+(8-2)*2÷3”转换规则的模拟过程如表1所示:
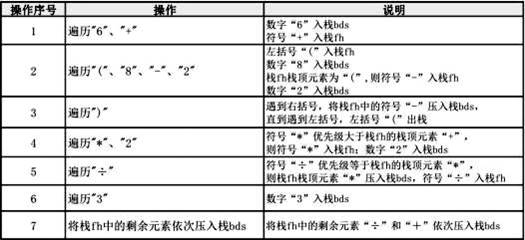 表 1
表 1
结合表1的操作过程,用栈bds和栈fh记录每个操作后的栈内情况(见下图),那么在操作2中栈fh里有内容为(请从栈底到栈顶顺序书写)。

⑵设计算法
基于问题的抽象与建模,解决该问题的主要算法描述如下:
从左往右遍历四则运算式s(设中间变量为ch):
1)当ch是数字,直接入栈bds;
2)当ch是运算符:
a.若ch为左括号时,直接入栈fh;
b.若ch为右括号时,则将栈fh元素弹出,压入栈bds,直到遇到左括号(左括号只弹出,不压入栈bds);
c.若ch为其它运算符时,如果运算符ch优先级大于栈fh中栈顶元素的优先级(或栈fh为空),直接入栈fh;否则,将栈fh元素依次弹出,并压入栈bds,直到运算符ch优先级大于栈fh中栈顶元素的优先级(或栈fh为空);
3)将栈bds中元素依次出栈,即为该四则运算s的后缀表达式。
⑶编写程序
实现上述功能的 Python 代码如下,请在划线处填入合适代码。
yxj = {"+":1,"-":1,"*":2,"÷":2} #运算规则的优先级
s = input("请输入四则运算式: ")
fh = [""]*100 #存储运算符
topfh = -1
bds = [""]*100 #存储表达式
top=-1
for ch in s:
if ch.isdigit(): #字符串只包含数字则返回 True 否则返回 False
top+=1
bds[top]=ch
elif ch == "(":
topfh +=1
fh[topfh]=ch
elif ch == ")":
while True:
tmp = fh[topfh]
topfh-=1
if tmp=="(":
top+=1
bds[top]=tmp
elif ch in yxj:
if topfh==-1 or fh[topfh]=="(":
topfh += 1
fh[topfh]=ch
elif :
topfh+=1
fh[topfh]=ch
else:
while fh[topfh]!="(" and topfh!=-1:
if yxj[fh[topfh]]>=yxj[ch]:
top+=1
bds[top]=fh[topfh]
topfh-=1
else:
break
topfh+=1
while topfh!=-1:
top+=1
bds[top]=fh[topfh]
topfh-=1
print("后缀表达式:","".join(bds[:top+1]))