1. (2022七下·济南期末) 问题发现：若x满足（9﹣x）（x﹣4）＝2，求（9﹣x）²+（x﹣4）²的值．

小明在解决该问题时，采用了以下解法：

解：设（9﹣x）＝a，（x﹣4）＝b，

则ab＝（9﹣x）（x﹣4）＝  ▲   ， a+b＝（9﹣x）+（x﹣4）＝  ▲   ．

所以（9﹣x）²+（x﹣4）²＝a²+b²＝（a+b）²﹣2ab＝  ▲   ．

1. （1） 请补全小明的解法；
3. （2） 已知（30﹣x）（x﹣20）＝﹣10，则（30﹣x）²+（x﹣20）²的值为 ．
5. （3） 若x满足（2023﹣x）²+（x﹣2021）²＝2022，求（2023﹣x）（x﹣2021）的值．
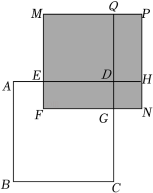
7. （4） 如图，正方形ABCD的边长为x，AE＝1，CG＝3，长方形EFGD的面积是10，分别以DE、DG为边长作正方形MEDQ和NGDH，PQDH是长方形，求图中阴影部分的面积为（结果必须是一个具体数值）．