-
-
(1)
已知

,

,

为

的三边长,且有

试判断

的形状并加以证明.
-
-
(2)
已知

,

满足

, 且

,

都是整数,求

的值.
-
-
(3)
在平面直角坐标系中,已知点

,

, 在

轴上求一点

, 使得

是等腰三角形,求

点的坐标

画图,在图上标出坐标

-
-
(4)
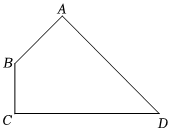
如图,在四边形

中,

,

,

,

, 在

、

上分别找一点

、

, 使得

的周长最小,求

周长的最小值.
-
-
(5)
我们定义:如果两个多项式

与

的和为常数,则称

与

互为“对消多项式”,这个常数称为它们的“对消值”

如

与

互为“对消多项式”,它们的“对消值”为

已知关于

的多项式

与

互为“对消多项式”,“对消值”为

若

,

, 求代数式

的最小值.
-

微信扫码预览、分享更方便
