【背景】已知： ∥m∥n∥k ，平行线与m、m与n、n与k之间的距离分别为d1 ， d2 ， d3 ，且d1＝d3＝1，d2＝2.我们把四个顶点分别在，m ， n ， k这四条平行线上的四边形称为“格线四边形”

1. (2018八下·江都月考) 【背景】已知： $\text{[math]}$ ∥m∥n∥k ，平行线 $\text{[math]}$ 与m、m与n、n与k之间的距离分别为d₁ ， d₂ ， d₃ ，且d₁＝d₃＝1，d₂＝2.我们把四个顶点分别在 $\text{[math]}$ ，m ， n ， k这四条平行线上的四边形称为“格线四边形” ．
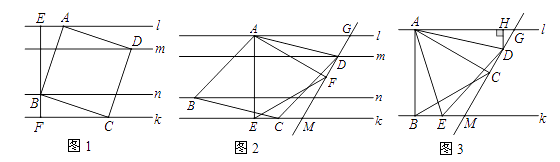
1. （1）【探究1】如图1，正方形ABCD为“格线四边形”，BE⊥ $\text{[math]}$ 于点E ， BE的反向延长线交直线k于点F.求正方形ABCD的边长．
3. （2）【探究2】如图2，菱形ABCD为“格线四边形”且∠ADC＝60°，△AEF是等边三角形，AE⊥k于点E ， ∠AFD＝90°，直线DF分别交直线 $\text{[math]}$ ，k于点G、点M.求证：EC＝DF ．
5. （3）【拓展】如图3， $\text{[math]}$ ∥k ，等边△ABC的顶点A ， B分别落在直线 l ， k上，AB⊥k于点B ，且∠ACD＝90°，直线CD分别交直线 $\text{[math]}$ 、k于点G、点M ，点D、点E分别是线段GM、BM上的动点，且始终保持AD＝AE ， DH⊥ $\text{[math]}$ 于点H.猜想：DH在什么范围内，BC∥DE？并说明此时BC∥DE的理由．

微信扫码预览、分享更方便

1. (2018八下·江都月考) 【背景】已知： ∥m∥n∥k ， 平行线 与m、m与n、n与k之间的距离分别为d1 ， d2 ， d3 ， 且d1＝d3＝1，d2＝2.我们把四个顶点分别在 ，m ， n ， k这四条平行线上的四边形称为“格线四边形” ．