 B .
B .  C .
C .  D .
D . 
如图所示,虚线为静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面3的电势为0.一带正电的点电荷在静电力的作用下运动,经过a、b点时的动能分别为26eV和5eV.当这一点电荷运动到某一位置,其电势能变为﹣8eV时,它的动能应为( )

如图所示,在光滑绝缘的水平地面上,固定着三个质量相等的带电小球a、b、c,三球在一条直线上,若释放a球,a球初始加速度为1m/s2 , 方向向左,若释放c球,c球初始加速度为3m/s2 , 方向向右,当释放b球时,b球的初始加速度应是( )

B组:空间存在一匀强磁场B,其方向垂直纸面向里,另有一个点电荷+Q的电场,如图所示,一带电﹣q的粒子以初速度v0从某处垂直电场、磁场入射,初位置到点电荷的距离为r,则粒子在电磁场中的运动轨迹可能为( )

为了使测量结果更准确,测量前应进行如下两项操作:先换用挡(填“×10”或“×1000”),接着进行(填“机械调零”或“欧姆调零”),然后再进行测量并读数.下图为一正在测量中的多用电表表盘.

在测量电源的电动势和内阻的实验中,由于所用的电压表(视为理想电压表)的量程较小,某同学设计了如图所示的实物电路.

①实验时,应先将电阻箱的电阻调到.(选填“最大值”、“最小值”或“任意值”)
②改变电阻箱的阻值R,分别测出阻值R0=10Ω的定值电阻两端的电压U,下列两组R的取值方案中,比较合理的方案是.(选填1或2)
方案编号 | 电阻箱的阻值R/Ω | ||||
1 | 400.0 | 350.0 | 300.0 | 250.0 | 200.0 |
2 | 80.0 | 70.0 | 60.0 | 50.0 | 40.0 |
③根据实验数据描点,绘出的 图象是一条直线.若直线的斜率为k,在
坐标轴上的截距为b,则该电源的电动势E=,内阻r=(用k、b和R0表示).
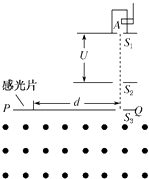
如图所示是质谱仪的工作原理示意图.设法使某种电荷量为q的正离子导入容器A中,离子再从狭缝S1飘入电压为U的加速电场,初速度不计.再通过狭缝S2、S3射入磁感应强度为B的匀强磁场中,射入方向垂直于磁场区的界面PQ.最后离子打到感光片上,形成垂直于纸面且平行于狭缝S3的细线.若测得细线到狭缝S3的距离为d,请导出离子的质量m的表达式.
如图,由A、B两平行金属板构成的电容器放置在真空中,电容为C,原来不带电.电容器的A板接地,并且中心有一个小孔,通过这个小孔向电容器中射入电子,射入的方向垂直于极板,射入的速度为v0 , 如果电子的发射是一个一个地单独进行,即第一个电子到达B板后再发射第二个电子,并且所有到达板的电子都留在B板上.随着电子的射入,两极板间的电势差逐渐增加,直至达到一个稳定值,已知电子的质量为m,电荷量为q,电子所受的重力忽略不计,两板的距离为l.

如图甲所示,在光滑绝缘的水平桌面上建立xOy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一个质量为10g、电荷量为0.1C且不计重力的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2πT.求:
