①36的平方根是6; ②±9的平方根是±3; ③ =±4; ④0.01是0.1的平方根; ⑤42的平方根是4; ⑥81的算术平方根是±9.
其中正确的说法是( )

成绩 | 6 | 7 | 8 | 9 | 10 |
人数 |
| 正 一 | 正 正 一 | 正 正
| 正 |
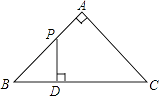
如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
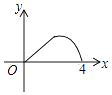 B .
B . 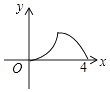 C .
C . 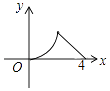 D .
D . 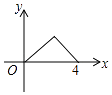


11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 |
2 | 8 | 10 | 17 | 6 | 13 | 7 | 5 | 7 | 3 |
12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |

如图,已知直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于E和F.
