| x | 196 | 197 | 200 | 203 | 204 |
| y | 1 | 3 | 6 | 7 | m |
7327 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
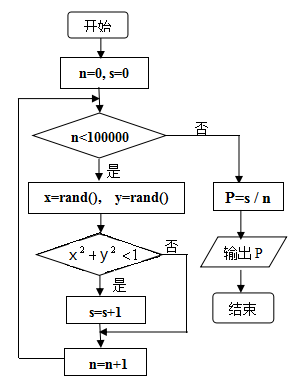
根据以上数据估计该运动员射击4次至少击中3次的概率为.
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54

①从匀速传递的产品生产流水线上,每20分钟从中抽取一件产品进行检测,这样的抽样是分层抽样。②两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1。
③在线性回归方程 中,当解释变量
每增加一个单位时,预报变量
平均增加0.2个单位。④分类变量
与
,它们的随机变量
的观测值为
,当
越小,“
与
有关系”的把握程度越大。
492 496 494 495 498 497 501 502 504 496
497 503 506 508 507 492 496 500 501 499
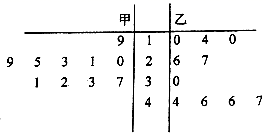
根据频率分布估计总体分布的原理,该自动包装机包装的袋装食盐质量在 之间的概率约为.
|
组别 |
一 |
二 |
三 |
四 |
五 |
|
候车时间(分钟) |
| | | | |
| 人数 | 2 | 6 | 4 | 2 | 1 |
第一步,一次性随机抽取2件,若都合格则整箱产品检验通过;若都不合格则整箱产品检验不通过,检验结束,剩下的产品不再检验.若抽取的2件产品有且仅有1件合格,则进行第二步工作.
第二步,从剩下的8件产品中再随机抽取1件,若不合格,则整箱产品检验不通过,检验结束,剩下的产品不再检验.若合格,则进行第三步工作.
第三步,从剩下的7件产品中随机抽取1件,若不合格,则整箱产品检验不通过,若合格,则整箱产品检验通过,检验结束,剩下的产品都不再检验.
假设某箱该产品中有8件合格品,2件次品.
(Ⅰ)求该箱产品被检验通过的概率;
(Ⅱ)若每件产品的检验费用为10元,设该箱产品的检验费用和检验不通过的损失费用之和为 ,求
的分布列和数学期望
.
Ⅰ
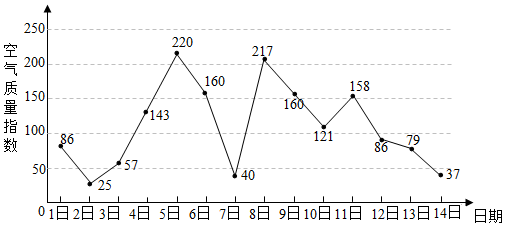
求此人到达当日空气质量优良的概率;
Ⅱ
求此人在该市停留期间只有1天空气重度污染的概率;
Ⅲ
由图判断从哪天开始连续三天的空气质量指数方差最大?
结论不要求证明
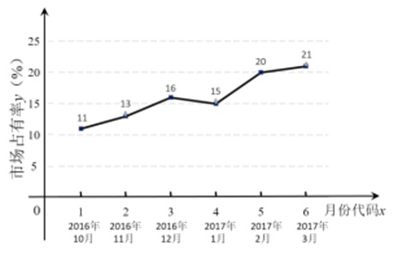
参考公式:回归直线方程为 ,其中
,
.
| 寿命 车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
| A | 20 | 35 | 35 | 10 | 100 |
| B | 10 | 30 | 40 | 20 | 100 |
经测算,平均每辆单车每年可以带来收入500元,不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率,如果你是 公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?