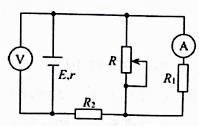
如图所示,在竖直放置的平行板电容器的金属板内侧表面系一绝缘细线,细线下端系一带电小球,带电小球静止时绝缘细线与金属板的夹角为θ.电容器接在如图所示的电路中,R1为电阻箱,R2为滑动变阻器,R3为定值电阻.闭合开关S,此时R2的滑片在正中间,电流表和电压表的示数分别为I和U.已知电源电动势E和内阻r一定,电表均为理想电表.以下说法正确的是( )

在图甲所示的电路中,电源的电动势为3.0V,内阻不计,灯L1、L2、L3为三个相同规格的小灯泡,这种小灯泡的伏安特性曲线如图乙所示.当开关闭合后,下列说法中正确的是( )




如图所示的电路中,定值电阻R的阻值大于电源内阻r的阻值,将滑动变阻器滑片向下滑动,理想电压表V1、V2、V3示数变化量的绝对值分别为△U1、△U2、△U3 , 理想电流表A示数变化量的绝对值为△I,则( )

如图所示,a、b端输入恒定的交流电压。理想变压器原、副线圈分别接有额定电压均为12V,额定功率均为2W的灯泡A,B,C。闭合开关,灯泡均正常发光。则下列说法正确的是( )


如图甲所示,理想变压器原、副线圈的匝数比为4:1,电压表和电流表均为理想电表,原线圈接如图乙所示的正弦交流电,图中Rt为热敏电阻,R为定值电阻.下列说法正确的是( )

如图所示,导电物质为电子的霍尔元件位于两串联线圈之间,线圈中电流为I,线圈间产生匀强磁场,磁感应强度大小B与I成正比,方向垂直于霍尔元件的两侧面,此时通过霍尔元件的电流为IH , 与其前后表面相连的电压表测出的霍尔电压UH满足:UH= ,式中k为霍尔系数,d为霍尔元件两侧面间的距离,电阻R远大于RL , 霍尔元件的电阻可以忽略,则( )

A.量程0~3 V,内阻约1 000 Ω的电压表
B.量程0~15 V,内阻约1 500 Ω的电压表
C.总阻值为10 Ω、额定电流为2 A的滑动变阻器
D.总阻值为100 Ω、额定电流为1 A的滑动变阻器
请在方框内完成实验电路图;

A. 电流表A1(量程0--0.3 A,内阻约为5 Ω)
B. 电流表A2(量程0--0.6 A,内阻约为1 Ω)
C. 电压表V1(量程0--3 V,内阻约3 kΩ)
D. 电压表V2(量程0--15 V,内阻约18 kΩ)
E. 定值电阻R0=5Ω
F. 滑动变阻器R1(总阻值5Ω)
G. 滑动变阻器R2(总阻值100Ω)
H. 电源(电动势E=6 V,内阻约为1Ω)
I. 开关和导线若干.


经典电磁理论认为:当金属导体两端电压稳定后,导体中产生恒定电场,这种恒定电场的性质与静电场相同.由于恒定电场的作用,导体内自由电子定向移动的速率增加,而运动过程中会与导体内不动的粒子发生碰撞从而减速,因此自由电子定向移动的平均速率不随时间变化.金属电阻反映的是定向运动的自由电子与不动的粒子的碰撞.假设碰撞后自由电子定向移动的速度全部消失,碰撞时间不计.
某种金属中单位体积内的自由电子数量为n,自由电子的质量为m,带电量为e.现取由该种金属制成的长为L,横截面积为S的圆柱形金属导体,将其两端加上恒定电压U,自由电子连续两次与不动的粒子碰撞的时间间隔平均值为t0 . 如图所示.

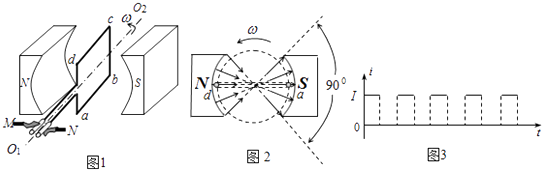
有人为汽车设计的一个“再生能源装置”原理简图如图1所示,当汽车减速时,线圈受到磁场的阻尼作用帮助汽车减速,同时产生电能储存备用.图1中,线圈的匝数为n,ab长度为L1 , bc长度为L2 . 图2是此装置的侧视图,此时cd边靠近N极,切割处磁场的磁感应强度大小恒为B,有理想边界的两个扇形磁场区夹角都是900 . 某次测试时,外力使线圈以角速度ω逆时针匀速转动,电刷M端和N端接电流传感器,电流传感器记录的i﹣t图象如图3所示(I为已知量),取ab边刚开始进入左侧的扇形磁场时刻t=0.不计线圈转动轴处的摩擦