一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
-
A . {1,2,3}
B . {1,2,4}
C . {2,3,4}
D . {1,2,3,4}
-
A .  B . 3i
C .
B . 3i
C .  D . -4+3i
D . -4+3i
-
A . 若  且
且  ,则
,则  B . 若
B . 若  且
且  ,则
,则  C . 若
C . 若  且
且  ,则
,则  D . 若
D . 若  不垂直于
不垂直于  ,且
,且  ,则
,则  不垂直于
不垂直于 
-
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分与不必要条件
-
-
-
7.
(2019·浙江模拟)
已知双曲线 C:

的左、右焦点分别为 F
1 , F
2 ,过F
2作双曲线C的一条渐近线的垂线,垂足为H,若F
2H的中点M在双曲线C上,则双曲线C的离心率为( )
A .  B .
B .  C . 2
D . 3
C . 2
D . 3
-
8.
(2019·浙江模拟)
甲盒子装有3个红球,1个黄球,乙盒中装有1个红球,3个黄球,同时从甲乙两盒中取出i(i=1,2,3)个球交换,分别记甲乙两个盒子中红球个数的数学期望为E
1(i),E
2(i),则以下结论错误的是( )
A . E1(1)>E2(1)
B . E1(2)=E2(2)
C . E1(1)+E2(1) =4
D . E1(3)<E2(1)
-
-
10.
(2019·浙江模拟)
已知正四面体

中,

为

的中点,则过点

与侧面

和底面

所在平面都成

的平面共有( )(注:若二面角

的大小为

,则平面

与平面

所成的角也为

)
A . 1个
B . 2个
C . 3个
D . 4个
二、填空题(本大题共7小题,多空题每小题6分,单空题每小题4分,共36分.)
-
-
12.
(2019·浙江模拟)
已知实数

,

满足不等式组

则

的最小值为
;当

的最大值为

时,实数

的值为
.
-
-
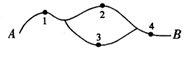
14.
(2019·浙江模拟)
如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有
种.
-
-
16.
(2019·浙江模拟)
已知直角三角形ABC中,直角边AC=6,点D是边AC上一定点,CD=2,点P是斜边AB上一动点,CP⊥BD,则△

面积的最大值是
;线段

长度的最小值是
.
-
三、解答题(本大题共5小题,共74分。解答应写出文字说明、证明过程或演算步骤.)
-
-
19.
(2019·浙江模拟)
等边三角形ABC的边长为

,点D、E分别是边AB、AC上的点,且满足

(如图1).将△ADE沿DE折起到△A
1DE的位置,使二面角A
1-DE-B成直二面角,连结A
1B、A
1C (如图2).
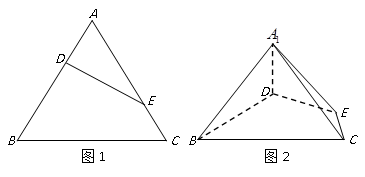
(Ⅰ)求证:A1D  平面BCED;
平面BCED;
(Ⅱ)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角为60°?若存在,求出PB的长,若不存在,请说明理由.
-
20.
(2019·浙江模拟)
在数列

中,

,其中实数

.
(Ⅰ)求  的通项公式;
的通项公式;
(Ⅱ)若对一切  有
有  ,求
,求  的取值范围.
的取值范围.
-
21.
(2019·浙江模拟)
如图,已知点

为抛物线

的焦点,过点

任作两条互相垂直的直线

,分别交抛物线

于

四点,

分别为

的中点.

(Ⅰ)求证:直线  过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(Ⅱ)设直线  交抛物线
交抛物线  于
于  两点,试求
两点,试求  的最小值.
的最小值.
-
22.
(2019·浙江模拟)
设

,已知函数

存在极大值.
(Ⅰ)若  =1,求b的取值范围;
=1,求b的取值范围;
(Ⅱ)求  的最大值,使得对于b的一切可能值,
的最大值,使得对于b的一切可能值,  的极大值恒小于0.
的极大值恒小于0.



平面BCED;

过定点,并求出该定点的坐标;
交抛物线
于
两点,试求
的最小值.