 B .
B . 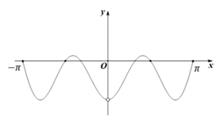 C .
C . 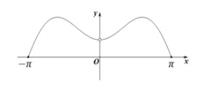 D .
D . 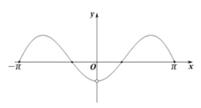
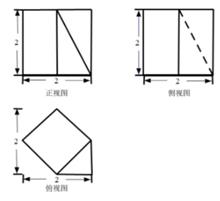
(Ⅰ) =,
(Ⅱ)若c=10,角C的平分线CM交边AB于点M,且|CM|=4,则b= .
(Ⅰ)求函数f(x)的解析式,并写出f(x)单调递减区间;
(Ⅱ)设函数s(x)=f(x- ),求g(x)在区间[
,
]上的值域。
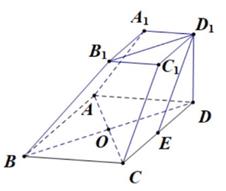
(Ⅰ)求证:直线AC⊥平面BDD1B1;
(Ⅱ)求直线ED1与平面ABB1A1所成角的正弦值。
(Ⅰ)求证:数列{bn+1 , -bn}是等比数列;
(Ⅱ)求数列{an}与{bn}的通项公式;
(Ⅲ)设cn= ,数列{cn}的前n项和为了Tn , 求证:Tn<

(Ⅰ)求证:切线PA的方程是x1x+2y1y-2=0;
(Ⅱ)设点P为抛物线D:y=x2+2上的动点,求△PAB面积的最小值.
(Ⅰ)若直线y=ax是曲线y=f(x)的切线,求a2b的最大值;
(Ⅱ)设b=1,若函数f(x)有两个极值点高与x,且x1<x2 , 求 的取值范围.