在中轴线竖直且固定的光滑圆锥形容器中,固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小环可以自由转动,但不能上下移动),小环上连接了一轻绳,与一质量为m的光滑小球相连,让小球在圆锥内作水平面上的匀速圆周运动,并与圆锥内壁接触,如图所示,图(a)中小环与小球在同一水平Ian上,图(b)中轻绳与竖直轴成θ角,设(a)图和(b)图中轻绳对小球的拉力分别为Ta和Tb , 圆锥内壁对小球的支持力分别为Na和Nb , 则在下列说法中正确的是( )

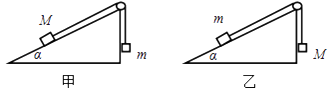
质量分别为M和m的物块形状大小均相同,将它们通过轻绳跨过光滑定滑轮连接,如图甲所示,绳子平行于倾角为α的斜面,M恰好能静止在斜面上,不考虑M、m与斜面之间的摩擦,若互换两物块位置,按图乙放置,然后释放M,斜面仍保持静止,则下列说法正确的是( )
如图,竖直平面内有一段圆弧MN,小球从圆心O处水平抛出,若初速度为va , 将落在圆弧上的a点,若初速度为vb , 将落在圆弧上的b点,已知Oa、Ob与竖直方向的夹角分别为α、β,不计空气阻力,则初速度大小之比为( )

如图所示,电源电动势为E,内阻为r.电路中的R2、R3分别为总阻值一定的滑动变阻器,R0为定值电阻,R1为光敏电阻(其电阻随光照强度增大而减小).当电键S闭合时,电容器中一带电微粒恰好处于静止状态.有关下列说法中正确的是( )

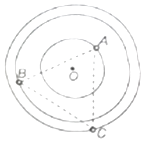
宇宙空间由一种由三颗星体A、B、C组成的三星体系,它们分别位于等边三角形ABC的三个顶点上,绕一个固定且共同的圆心O做匀速圆周运动,轨道如图中实线所示,其轨道半径rA<rB<rC . 忽略其他星体对它们的作用,可知这三颗星体( )
如图所示,光滑水平面内固定有一槽,一轻杆一端处于槽内,另一端与一轻质弹簧相连,当左边物块撞击弹簧时,若弹簧的压缩量超过某一值,轻杆可以在槽内移动,设杆在槽内移动时所受到的摩擦力大小恒为f,现有一质量为m的物块以某一初速度v0撞击轻质弹簧,最后物块以速度v被弹簧反射回来,弹簧在压缩过程中始终处于弹性限度内,且物块与弹簧作用时没有能力损失,则下列说法正确的是( )

根据图甲实验电路,请在图乙中用笔画线代替导线,完成实物电路图.

合上开关S1 , S2接图甲中的1位置,滑动滑片P,记录下几组电压表和电流表的示数,重置滑动变阻器,S2改接图甲中的2位置,滑动滑片P,再记录几组电压表和电流表的示数,在同一坐标系内分别描点作出S2接1、2位置时电压表示数U和电流表示数I的图象,如图丙所示,两图线均为直线,与纵轴的截距分别为UA、UB , 与横轴的截距分别为IA、IB .

①S2接1位置时,作出的U﹣I图线是图丙中的(填“A”或“B”);
②S2接2位置时,干电池电动势的测量值真实值,内阻的测量值真实值.(填“大于”、“小于”或“等于”)
如图甲所示,在水平放置的气垫导轨上有一带有方盒的滑块,质量为M,气垫导轨右端固定一定滑轮,细线绕过滑轮,一端与滑块相连,另一端挂有6个钩码,设每个钩码的质量为m,且M=4m.
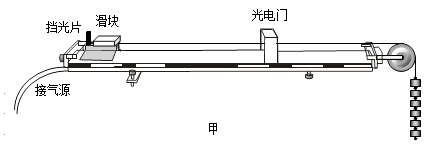
用游标卡尺测出滑块上的挡光片的宽度,读数如图乙所示,则宽度d=cm;
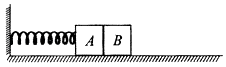
如图所示,质量均为m=3kg的物块A、B紧挨着放置在粗糙的水平地面上,物块A的左侧连接一劲度系数为k=100N/m的轻质弹簧,弹簧另一端固定在竖直墙壁上,开始时两物块压紧弹簧并恰好处于静止状态,现使物块B在水平外力F作用下向右做a=2m/s2的匀加速直线运动直至与A分离,已知两物块与地面间的动摩擦因数均为0.5,最大静摩擦力等于滑动摩擦力,g=10m/s2 , 求:
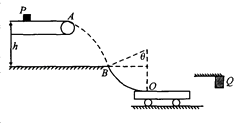
如图所示,质量为m=1kg的可视为质点的小物块轻轻放在水平匀速运动的传送带上的P点,随传送带运动到A点后水平抛出,小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑圆弧轨道下滑,圆弧轨道与质量为M=2kg的足够长的小车左端在最低点O点相切,并在O点滑上小车,水平地面光滑,当物块运动到障碍物Q处时与Q发生无机械能损失的碰撞,碰撞前物块和小车已经相对静止,而小车可继续向右运动(物块始终在小车上),小车运动过程中和圆弧无相互作用.已知圆弧半径R=1.0m,圆弧对应圆心角的θ为53°,A点距水平面的高度h=0.8m,物块与小车间的动摩擦因数为μ=0.1,重力加速度g=10m/s2 , sin53°=0.8,cos53°=0.6.试求:
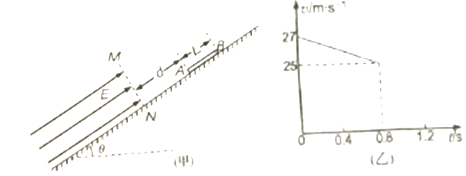
如图甲所示,倾角为θ=30°绝缘斜面被垂直斜面直线MN分为左右两部分,左侧部分光滑,范围足够大,上方存在大小为E=1000N/C,方向沿斜面向上的匀强电场,右侧部分粗糙,范围足够大,一质量为m=1kg,长为L=0.8m的绝缘体制成的均匀带正电直棒AB置于斜面上,A端距MN的距离为d,现给棒一个眼斜面向下的初速度v0 , 并以此时作为计时的 起点,棒在最初0.8s的运动图象如图乙所示,已知0.8s末棒的B端刚好进入电场,取重力加速度g=10m/s2 , 求: