2016-2017学年重庆市荣昌县盘龙中学平行班八年级下学期...

更新时间：2017-07-26 浏览次数：1108 类型：期中考试

一、选择题

1. (2017八下·荣昌期中) 若 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是（）

A . x≥ $\text{[math]}$ B . x≥﹣ $\text{[math]}$ C . x＞ $\text{[math]}$ D . x≠ $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八下·西山月考) 一直角三角形的两直角边长为12和16，则斜边长为（）

A . 12 B . 16 C . 18 D . 20

答案解析收藏纠错 + 选题
3. (2017八下·荣昌期中) 一次函数y=﹣ $\text{[math]}$ x+1的图象不经过的象限是（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
4. (2017八下·蒙阴期末) 下列计算错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八下·丰南期中) 如图，点P是平面坐标系中一点，则点P到原点的距离是（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八上·青浦期末) 下列根式中，是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023·黄冈模拟) 如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（）

A . 当AB=BC时，它是菱形 B . 当AC⊥BD时，它是菱形 C . 当∠ABC=90°时，它是矩形 D . 当AC=BD时，它是正方形

答案解析收藏纠错 + 选题
8. (2019八下·广安期中) 已知菱形ABCD中，对角线AC与BD交于点O，∠BAD=120°，AC=4，则该菱形的面积是（）

A . 16 $\text{[math]}$ B . 16 C . 8 $\text{[math]}$ D . 8

答案解析收藏纠错 + 选题
9. (2017八下·荣昌期中) 如图，E是正方形ABCD的边DC上一点，过点A作FA=AE交CB的延长线于点F，若AB=4，则四边形AFCE的面积是（）

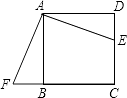
A . 4 B . 8 C . 16 D . 无法计算

答案解析收藏纠错 + 选题
10. (2017八下·荣昌期中) 如图，四边形ABCD中，AB=BC，∠ABC=∠CDA=90°，BE⊥AD于点E，且四边形ABCD的面积为8，则BE=（）

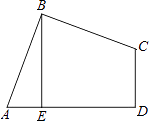
A . 2 B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2017八下·荣昌期中)
如图，用火柴棒摆出一列正方形图案，第①个图案用了4根，第②个图案用了12根，第③个图案用了24根，按照这种方式摆下去，摆出第⑥个图案用火柴棒的根数是（）

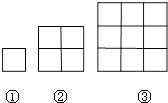
A . 84 B . 81 C . 78 D . 76

答案解析收藏纠错 + 选题
12. (2017八下·荣昌期中)
一次函数y₁=kx+b与y₂=x+a的图象如图所示，则下列结论：①k＜0；②a＜0，b＜0；③当x=3时，y₁=y₂；④不等式kx+b＞x+a的解集是x＜3，其中正确的结论个数是（）

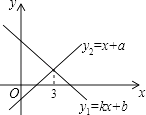
A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题

二、填空

13. (2024八下·武城期中) 已知 $\text{[math]}$ ，则x+y=．

答案解析收藏纠错 + 选题
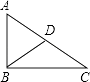
14. (2017八下·濮阳期中) 如图，已知△ABC中，AB=5cm，BC=12cm，AC=13cm，那么AC边上的中线BD的长为cm．

答案解析收藏纠错 + 选题
15. (2017八下·荣昌期中) 写出同时具备下列两个条件的一次函数表达式：（写出一个即可）．
①y随着x的增大而减小；
②图象经过点（0，﹣3）．

答案解析收藏纠错 + 选题
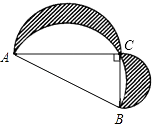
16. (2017八下·荣昌期中) 如图Rt△ABC中，AC=12，BC=5，分别以AB，AC，BC为直径作半圆，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题
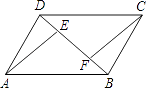
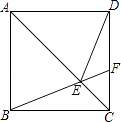
17. 如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E．若∠CBF=20°，则∠AED等于度．

答案解析收藏纠错 + 选题
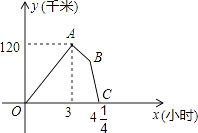
18. (2017八下·荣昌期中) 某物流公司的快递车和货车同时从甲地出发，以各自的速度匀速向乙地行驶，快递车到达乙地后缷完物品再另装货物共用45分钟，立即按原路以另一速度匀速返回，直至与货车相遇．已知货车的速度为60千米/时，两车之间的距离y（千米）与货车行驶时间x（小时）之间的函数图象如图所示，现有以下4个结论：
①快递车从甲地到乙地的速度为100千米/时；
②甲、乙两地之间的距离为120千米；
③图中点B的坐标为（3 $\text{[math]}$ ，75）；
④快递车从乙地返回时的速度为90千米/时，
以上4个结论正确的是．

答案解析收藏纠错 + 选题

三、解答题：解答时每小题必须给出必要的演算过程或推理步骤

19. (2017八下·荣昌期中) 计算：2 $\text{[math]}$ ×3 $\text{[math]}$ + $\text{[math]}$ +| $\text{[math]}$ ﹣1|﹣π⁰+（ $\text{[math]}$ ）^﹣¹ ．

答案解析收藏纠错 + 选题
20. (2017八下·荣昌期中) 如图所示，已知在平行四边形ABCD中，BE=DF．求证：∠DAE=∠BCF．

答案解析收藏纠错 + 选题

四、解答题：解答时每小题都必须写出必要的演算过程或推理步骤．

21. (2024七下·潮南期末) 先化简，后计算： $\text{[math]}$ ，其中a= $\text{[math]}$ ，b= $\text{[math]}$ ．

答案解析收藏纠错 + 选题
22. (2017八下·荣昌期中) 已知一次函数的图象a过点M（﹣1，﹣4.5），N（1，﹣1.5）
1. （1）求此函数解析式，并画出图象；
2. （2）求出此函数图象与x轴、y轴的交点A、B的坐标；
3. （3）若直线a与b相交于点P（4，m），a、b与x轴围成的△PAC的面积为6，求出点C的坐标．
答案解析收藏纠错 + 选题
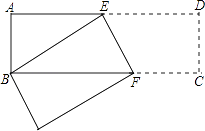
23. (2017八下·荣昌期中) 如图，长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF．求△ABE的面积．

答案解析收藏纠错 + 选题
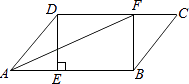
24. (2017·金乡模拟) 在▱ABCD中，过点D作DE⊥AB于点E，点F在边CD上，DF=BE，连接AF，BF．
1. （1）求证：四边形BFDE是矩形；
2. （2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB．
答案解析收藏纠错 + 选题

五、解答题：解答时每小题都必须写出必要的演算过程或推理步骤．

25. (2017八下·荣昌期中) 定义：如果M个不同的正整数，对其中的任意两个数，这两个数的积能被这两个数的和整除，则称这组数为M个数的祖冲之数组．如（3，6）为两个数的祖冲之数组，因为3×6能被（3+6整除）；又如（15，30，60）为三个数的祖冲之数组，因为（15×30）能被（15+30）整除，（15×60）能被（15+60）整除，（30×60）能被（30+60）整除…
1. （1）我们发现，3和6，4和12，5和20，6和30…，都是两个数的祖冲之数组；由此猜测n和n（n﹣1）（n≥2，n为整数）组成的数组是两个数的祖冲之数组，请证明这一猜想．
2. （2）若（4a，5a，6a）是三个数的祖冲之数组，求满足条件的所有三位正整数a．
答案解析收藏纠错 + 选题
26. (2017八下·荣昌期中) 已知E，F分别为正方形ABCD的边BC，CD上的点，AF，DE相交于点G，当E，F分别为边BC，CD的中点时，有：①AF=DE；②AF⊥DE成立．
试探究下列问题：
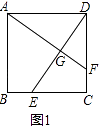
1. （1）
  如图1，若点E不是边BC的中点，F不是边CD的中点，且CE=DF，上述结论①，②是否仍然成立？（请直接回答“成立”或“不成立”），不需要证明）
2. （2）
  如图2，若点E，F分别在CB的延长线和DC的延长线上，且CE=DF，此时，上述结论①，②是否仍然成立？若成立，请写出证明过程，若不成立，请说明理由；
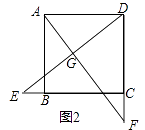
3. （3）
  如图3，在（2）的基础上，连接AE和EF，若点M，N，P，Q分别为AE，EF，FD，AD的中点，请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种，并证明你的结论．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2016-2017学年重庆市荣昌县盘龙中学平行班八年级下学期...

副标题：

*注意事项：

2016-2017学年重庆市荣昌县盘龙中学平行班八年级下学期...

试题分析

总体分析

题量分析

难度分析

知识点分析