
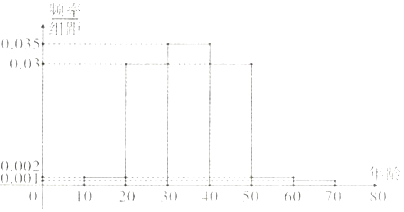
(Ⅰ)根据频率分布直方图,估计这组数据的中位数和平均值 (保留1位小数)
(Ⅱ)节目最后由高中生武亦姝和编辑彭敏争夺冠军,比赛规定:主持人每出一题,两位选手必有一人得1分,另一人不得分,先得5分者将成为第二季的总冠军,现比赛进行到武亦姝和彭敏的得分比为3:2,接下来假设主持人每出一道题,彭敏得分的概率为 ,武亦姝得分的概率为
,请问最终武亦姝获得冠军的概率是多少?
(Ⅲ)现从年龄在[10,20)、[50,60),[60,70]内的三组选手中任意抽取2人,求抽出选手中年龄大于50岁的人数ξ的概率分布列和期望.
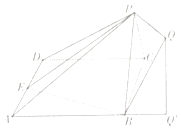
(Ⅰ)求证面PBC⊥面PBE
(Ⅱ)求平面PBQ与平面PAD所成钝二面角的正切值.
(Ⅰ)求E的方程;
(Ⅱ)若E的右焦点为F,圆x2+y2=1的切线AB与E交于A,B 两点(A,B均在y轴右侧),求证:△ABF的周长为定值,并求△ABF的内切圆半径的最大值.
(Ⅰ)设h(x)=f(x)﹣g(x),讨论函数h(x)的单调区间;
(Ⅱ)若f(x)﹣ax=0有两个不同实数解x1 , x2 , 求证:lnx1+lnx2>2.
(I )求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)当r为何值时,曲线C 上有且只有3个点到直线l的距离为1?