如图所示,长为L的细线,一端固定在O点,另一端系一个质量为m的小球,在最低点A给小球一个水平方向的瞬时冲量I,使小球绕悬点O在竖直平面内运动,为使细线始终不松弛,I的大小可选择下列四项中的( )
![]()
如图所示是某工厂所采用的小型生产流水线示意图,机器生产出的物体源源不断地从出口处以水平速度v0滑向一粗糙的水平传送带,最后从传送带上落下装箱打包.假设传送带静止不动时,物体滑到传送带右端的速度为v,最后物体落在P处的箱包中,下列说法正确的是( )
![]()
如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成了一个圆锥摆.关于摆球A的受力情况,下列说法中正确的是( )

如图1所示,用“碰撞实验器“可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系:

先安装好实验装置,在地上铺一张白纸,白纸上铺放复写纸,记下重垂线所指的位置O.
接下来的实验步骤如下:
步骤1:不放小球2,让小球1从斜槽上A点由静止滚下,并落在地面上.重复多次,用尽可能小的圆,把小球的所有落点圈在里面,其圆心就是小球落点的平均位置;
步骤2:把小球2放在斜槽前端边缘位置B,让小球1从A点由静止滚下,使它们碰撞.重复多次,并使用与步骤1同样的方法分别标出碰撞后两小球落点的平均位置;
步骤3:用刻度尺分别测量三个落地点的平均位置M、P、N离O点的距离,即线段OM、OP、ON的长度.
①对于上述实验操作,下列说法正确的是
A.应使小球每次从斜槽上相同的位置自由滚下
B.斜槽轨道必须光滑
C.斜槽轨道末端必须水平
D.小球1质量应大于小球2的质量
②上述实验除需测量线段OM、OP、ON的长度外,还需要测量的物理量有.
A.A、B两点间的高度差h1
B.B点离地面的高度h2
C.小球1和小球2的质量m1、m2
D.小球1和小球2的半径r
③当所测物理量满足表达式(用所测物理量的字母表示)时,即说明两球碰撞遵守动量守恒定律.如果还满足表达式(用所测物理量的字母表示)时,即说明两球碰撞时无机械能损失.
④完成上述实验后,某实验小组对上述装置进行了改造,如图2所示.在水平槽末端与水平地面间放置了一个斜面,斜面的顶点与水平槽等高且无缝连接.使小球1仍从斜槽上A点由静止滚下,重复实验步骤1和2的操作,得到两球落在斜面上的平均落点M′、P′、N′.用刻度尺测量斜面顶点到M′、P′、N′三点的距离分别为l1、l2、l3 . 则验证两球碰撞过程中动量守恒的表达式为(用所测物理量的字母表示).
小明研究小车在水平长木板上运动所受摩擦力的大小,选用的实验器材是:长木板、总质量为m的小车、光电门、数字毫秒计、弧形斜面、挡光片、游标卡尺、刻度尺.器材安装如图甲所示.

①用游标卡尺测量挡光片宽度d,读数如图乙所示,则d=mm.
②让小车从斜面上某一位置释放,读出小车通过光电门时数字毫秒计示数t.
③用刻度尺量出小车停止运动时遮光板与光电门间的距离L.
④求出小车与木板间摩擦力f=(用物理量的符号表示).
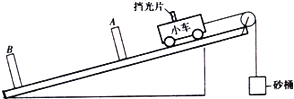
a.将长木板倾斜放置,小车放在长木板上,长木板旁放置两个光电门A和B,砂桶通过滑轮与小车相连.
b.调整长木板倾角,使得小车恰好能在细绳的拉力作用下匀速下滑.测得砂和砂桶的总质量为m.
c.某时刻剪断细绳,小车由静止开始加速运动.
d.测得挡光片通过光电门A的时间为△t1 , 通过光电门B的时间为△t2 , 挡光片宽度为d,小车质量为M,两个光电门A和B之间的距离为L.
e.依据以上数据探究动能定理.
如图所示,质量为m的物体A静止在地面上,其上表面竖直连接着一根长L、劲度系数为k的轻弹簧,现用手拉着弹簧上端P将物体缓慢提高h,则物体的重力势能增加了,人对弹簧拉力所做的功物体克服重力所做的功(填“大于”“小于”或“等于”).若弹簧的上端P点升高了H,物体恰已离开地面,则物体的重力势能增加了;人对弹簧拉力所做的功 mgH(填“大于”“小于”或“等于”).

如图所示,物体A放在足够长的木板B上,木板B静止于水平面.t=0时,电动机通过水平细绳以恒力F拉木板B,使它做初速度为零、加速度aB=1.0m/s2的匀加速直线运动.已知A的质量mA和B的质量mB均为2.0kg,A、B之间的动摩擦因数μ1=0.05,B与水平面之间的动摩擦因数μ2=0.1,最大静摩擦力与滑动摩擦力大小视为相等,重力加速度g取10m/s2 . 求

如图所示,质量为M=4kg的木板静止在光滑的水平面上,在木板的右端放置一个质量m=1kg大小可以忽略的铁块,铁块与木板之间的摩擦因数μ=0.4,在铁块上加一个水平向左的恒力F=8N,铁块在长L=6m的木板上滑动.取g=10m/s2 . 求:

如图所示,水平面O点的右侧光滑,左侧粗糙.O点到右侧竖直墙壁的距离为L,一系统由可看作质点的A、B两木块和一短而硬(即劲度系数很大)的轻质弹簧构成.A,B两木块的质量均为m,弹簧夹在A与B之间,与二者接触而不固连.让A、B压紧弹簧,并将它们锁定,此时弹簧的弹性势能为E0该系统在O点从静止开始在水平恒力F作用下幵始向右运动,当运动到离墙S=L/4时撤去恒力F,撞击墙壁后以原速率反弹,反弹后当木块A运动到O点前解除锁定.通过遥控解除锁定时,弹簧可瞬时恢复原长.求
