浙江省温州市育英国际实验学校2020届九年级数学中考模拟试卷...

更新时间：2024-07-13 浏览次数：308 类型：中考模拟

一、（共10小题，每小题4分，满分40分，在每小题给出的四个选项中，只有一个是符合题意的，请把正确的选项填在题后的括号内）

1. (2020·温州模拟) 在-6，0，2.5，|-3|这四个数中，最大的数是（）

A . -6 B . 0 C . 2.5 D . |-3|

答案解析收藏纠错 + 选题
2. (2020·温州模拟) 如右图所示，该几何体由两个圆柱分别从纵横两个方向嵌入一个正方体形成的，它的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2020·温州模拟) 下列计算正确的是（　　）

A . 2³=6 B . -4²=-16 C . -8-8=0 D . -5-2=-3

答案解析收藏纠错 + 选题
4. (2020·温州模拟) 根据温州市民政局社会事务处的历年数据显示，预计今年清明期间全市祭扫人数超310万人次，其中的310万用科学记数法表示为（）

A . 310×10⁴ B . 31×10⁵ C . 3.1x10⁶ D . 0.31×10⁷

答案解析收藏纠错 + 选题
5. (2022·牡丹模拟) 如图，已知△ABC与△DEF位似，位似中心为点O，且△ABC的面积等于△DEF面积的 $\text{[math]}$ ，则AO：AD的值为（）

A . 2：3 B . 2：5 C . 4：9 D . 4：13

答案解析收藏纠错 + 选题
6. (2020·温州模拟) 在一个不透明的袋中装有9个只有颜色不同的球，其中4个红球、3个黄球和2个白球,从袋中任意摸出一个球，不是白球的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020·温州模拟) 如图，一块矩形木板ABCD斜靠在墙边（OC⊥OB，点A，B，C，D，O在同一平面内）。已知AB=a，AD=b，∠BCO=θ，则点A到OC的距离等于（）

A . asinθ+bsinθ B . acosθ+bcosθ C . asinθ+bcosθ D . acosθ+bsinθ

答案解析收藏纠错 + 选题
8. (2020·温州模拟) 已知二次函数y=（x-1）²-1，关于该函数在0≤x≤3的取值范围内，下列说法正确的是（）

A . 有最小值0，有最大值3 B . 有最小值-1，有最大值0 C . 有最小值-1，有最大值3 D . 有最小值-1，无最大值

答案解析收藏纠错 + 选题
9. (2020·温州模拟) 如图，小靓用七巧板拼成一幅装饰图，放入长方形ABCD内，装饰图中的三角形顶点E， F分别在边AB，BC上，△GHD的边GD在边AD上，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020·温州模拟)
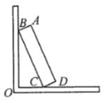
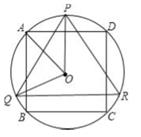
如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，反比例函数y= $\text{[math]}$ ，在第一象限内的图象经过点D，且与AB、BC分别交于E、F两点．若四边形BEDF的面积为6，则k的值为（　　）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每小题5分，共30分）

11. (2024七下·鄞州期末) 因式分解：a³－a=.

答案解析收藏纠错 + 选题
12. (2020·温州模拟) 一组数据2，x，1，3，5，4，若这组数据的中位数是3，则这组数据的方差是。

答案解析收藏纠错 + 选题
13. (2024九下·新会模拟) 已知扇形的半径为6，弧长为2π，则它的圆心角为度.

答案解析收藏纠错 + 选题
14. (2020·温州模拟) 如图，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O的内接正方形，BC∥QR，则∠AOQ=。

答案解析收藏纠错 + 选题
15. (2020·温州模拟) 已知正方形ABCD是边长为4，以AB为直径在正方形内作半圆，P是半圆上的动点（不与点A、B重合），连接PA、PB、PC、PD。把△PAD、△PAB、△PBC的面积分别记为S₁、S₂、S₃ ，则2S₁S₃-S₂²的最大值是。

答案解析收藏纠错 + 选题
16. (2020·温州模拟) 一个门环的示意图如图所示，图中以正六边形ABCDEF的对角线AC的中点O为圆心， OB为半径作⊙O，AQ切⊙O于点P，并交DE于点Q，若AQ=12 $\text{[math]}$ cm，则该圆的半径为cm。

答案解析收藏纠错 + 选题

三、解答题（本题有8小题，共80分．解答需写出必要的文字说明、演算步骤或证明过程）

17. (2020·温州模拟)
1. （1）计算：（π-3.14）⁰+（-2）^-1+sin30°
2. （2）化简：（x+2）²-x（x-4）
答案解析收藏纠错 + 选题
18. (2020·温州模拟) 如图，在Rt△ACB中，∠ACB=90°，点D是AB的中点，点E是CD的中点，过点C作CF∥AB交AE的延长线于点F。
1. （1）求证：△ADE≌△FCE；
2. （2）若∠DCF=120°，DE=2，求BC的长。
答案解析收藏纠错 + 选题
19. (2020·温州模拟) 随着通讯技术迅猛发展，人与人之间的沟通方式更多样、便捷．某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷（每人必选且只选一种），在全校范围内随机调查了部分学生，将统计结果绘制了如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：
1. （1）这次统计共抽查了名学生；在扇形统计图中，表示“QQ”的扇形圆心角的度数为；
2. （2）将条形统计图补充完整；
3. （3）该校共有1500名学生，请估计该校最喜欢用“微信”进行沟通的学生有多少名？
4. （4）某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系，请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率．
答案解析收藏纠错 + 选题
20. (2020·温州模拟) 图1，图2，图3是三张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，A，C两点都在格点上，连结AC，请完成下列作图：
1. （1）以AC为对角线在图1中作一个正方形，且正方形各顶点均在格点上
2. （2）以AC为对角线在图2中作一个矩形，使得矩形面积为6，且矩形各顶点均在格点上
3. （3）以AC为对角线在图3中作一个面积最小的平行四边形，且平行四边形各顶点均在格点上
答案解析收藏纠错 + 选题
21. (2020·温州模拟) 如图，在平面直角坐标系xOy中，抛物线y=ax²+bx+3的顶点为M（2，-1），交x轴与A、B两点，交y轴于点C，其中点B的坐标为（3，0）。
1. （1）求该抛物线的解析式；
2. （2）设经过点C的直线与该抛物线的另一个交点为D，且直线CD和直线CA关于直线CB对称，求直线CD的解析式。
答案解析收藏纠错 + 选题
22. (2020·温州模拟) 如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB于点F，连接BE.
1. （1）求证：AC平分∠DAB；
2. （2）求证：△PCF是等腰三角形；
3. （3）若tan∠ABC= $\text{[math]}$ ，求线段PC的长.
答案解析收藏纠错 + 选题
23. (2020·温州模拟) 疫情期间，某市制药厂需要紧急生产一批药品，要求必须在12天（含12天）内完成。为了加快生产，车间采取工人加班，机器不停的生产方式，这样每天药品的产量y（吨）是时间x（天）一次函数，且满足表中所对应的数量关系．由于机器负荷运转产生损耗，平均生产每吨药品的成本P（元）与时间x（天）的关系满足图中的函数图象。

时间x（天）

2

4

每天产量y（吨）

24

28
1. （1）求药品每天的产量y（吨）是时间x（天）之间的函数关系式；
2. （2）当5≤x≤12时，直接写出P（元）与时间x（天）的函数关系式：；
3. （3）若这批药品的价格为1400元/吨，每天的利润设为W元，求哪一天的利润最高，最高利润是多少？（利润=价格-成本）
4. （4）为了提高工人加班的津贴，药厂决定在（3）中价格的基础上每吨药品加价a元，但必须满足从第5天到第12天期间，每吨加价a后每天的利润随时间的增大而增大，直线写出a的最小值。
答案解析收藏纠错 + 选题
24. (2020·温州模拟) 如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（0，4），点B的坐标为（4，0），点C的坐标为（-4，0），点P在射线AB上运动，连结CP与y轴交于点D，连结BD．过P，D，B三点作⊙Q与y轴的另一个交点为E，延长DQ交⊙Q于点F，连结EF，BF。
1. （1）求直线AB的函数解析式；
2. （2）当点P在线段AB（不包括A，B两点）上时。
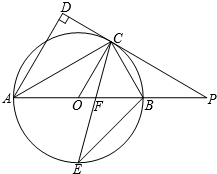
  ①求证：∠BDE=∠ADP；
  
  ②设DE=x，DF=y，请求出y关于x的函数解析式；
3. （3）点P在运动过程中，是否存在以B，D，F为顶点的直角三角形，满足两条直角边之比为2：1？如果存在，求出此时点P的坐标：如果不存在，请说明理由。
答案解析收藏纠错 + 选题