B . 
C . 
D . 
用台秤称量重物的质量
B . 
用水杯喝水
C . 
用沉淀法将水与沙子分离
D . 
给小球一个很小的初速度，小球即可以在竖直平面内做圆周运动
如图所示，质量为m的小球从距离地面高H的A点由静止开始释放，落到地面上后又陷入泥潭中，由于受到阻力作用到达距地面深度为h的B点速度减为零．不计空气阻力，重力加速度为g．关于小球下落的整个过程，下列说法中正确的有（ ）
如图所示，质量分别为m和2m的A、B两个木块间用轻弹簧相连，放在光滑水平面上，A靠紧竖直墙．用水平力F将B向左压，使弹簧被压缩一定长度，静止后弹簧储存的弹性势能为E．这时突然撤去F，关于A、B和弹簧组成的系统，下列说法中正确的是（ ）
如图所示为一皮带传动装置，在传动过程中皮带不打滑．a、b分别是小齿轮和大齿轮边缘上的点，c是大齿轮上某条半径上的中点，已知大齿轮的半径是小齿轮半径的2倍．若a点的线速度大小为v，则b点的线速度大小为，c点的线速度大小为．
一根长为l且不可伸长的轻质细绳，一端固定于O点，另一端拴一质量为m的小球．现将小球拉至细绳沿水平方向绷紧的状态，由静止释放小球，如图所示．若不考虑空气阻力的作用，重力加速度为g，则小球摆到最低点A时的速度大小为，此时绳对小球的拉力大小为．
A．重锤的质量
B．重锤下落的高度
C．重锤底部距水平地面的高度
D．与下落高度对应的重锤的瞬时速度
某同学用图甲所示装置通过半径相同的A、B两球的碰撞来寻找碰撞中的不变量，图中PQ是斜槽，QR为水平槽，实验时先使A球从斜槽上某一固定位置C由静止开始滚下，落到位于水平地面的记录纸上，留下痕迹，重复上述操作10次，得到10个落点痕迹，再把B球放在水平槽上靠近槽末端的地方，让A球仍从位置C由静止开始滚下，和B球碰撞后，A、B球分别在记录纸上留下各自的落点痕迹，重复这种操作10次，图中O是水平槽末端口在记录纸上的垂直投影点，Pˊ为未放被碰小球B时A球的平均落点，M为与B球碰后A球的平均落点，N为被碰球B的平均落点．若B球落点痕迹如图乙所示，其中米尺水平放置，且平行于O Pˊ，米尺的零点与O点对齐．
在物理学中，常常用等效替代、类比、微小量放大等方法来研究问题．如在牛顿发现万有引力定律一百多年后，卡文迪许利用微小量放大法由实验测出了万有引力常量G的数值，如图所示是卡文迪许扭秤实验示意图．卡文迪许的实验常被称为是“称量地球质量”的实验，因为由G的数值及其它已知量，就可计算出地球的质量，卡文迪许也因此被誉为第一个称量地球的人．
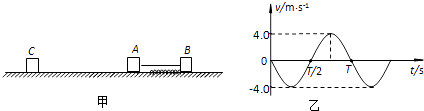
如图甲所示，三个物体A、B、C静止放在光滑水平面上，物体A、B用一轻质弹簧连接，并用细线拴连使弹簧处于压缩状态，此时弹簧长度L=0.1m；三个物体的质量分别为mA=0.1kg、mB=0.2kg和mC=0.1kg．现将细线烧断，物体A、B在弹簧弹力作用下做往复运动（运动过程中物体A不会碰到物体C）．若此过程中弹簧始终在弹性限度内，并设以向右为正方向，从细线烧断后开始计时，物体A的速度‒时间图象如图乙所示．求：
