江西省吉安市吉州区2019年中考数学5月模拟考试试卷

更新时间：2020-04-29 浏览次数：174 类型：中考模拟

一、单选题

1. (2019·吉安模拟) 2019的绝对值等于（）

A . ﹣2019 B . 2019 C . ﹣ $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019·吉安模拟) 如图几何体的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2019·吉安模拟) 今年3月，某校举行“唱红歌”歌咏比赛，有19位同学参加选拔赛，所得分数互不相同，按成绩取前9名进入决赛，若知道某同学分数，要判断他能否进入决赛，只需知道19位同学分数的（）

A . 中位数 B . 平均数 C . 极差 D . 方差

答案解析收藏纠错 + 选题
4. (2019·吉安模拟) 欧阳修在《卖油翁》中写道：“（翁）乃取一葫芦置于地，以钱覆其口，徐以构酌油之，自钱孔入，而钱不湿”，如图，可见卖油的技艺之高超，若铜钱直径4cm ，中间x有边长为1cm的正方形小孔，随机向铜色钱上滴一滴油（油滴大小忽略不计），则油恰好落入孔中的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2019·吉安模拟) 已知二次函数y＝2mx²+（1﹣m）x﹣1﹣m ，下面说法不正确是（）

A . 当m＝1时，函数图象的顶点坐标是（0，﹣2） B . 当m＝﹣1时，函数图象与x轴有两个交点 C . 函数图象经过定点（1，0），（﹣ $\text{[math]}$ ，﹣ $\text{[math]}$ ） D . 当m＞0时，函数图象截x轴所得的线段长度小于 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九下·渠县开学考) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 分别为 $\text{[math]}$ ， $\text{[math]}$ 的中点， $\text{[math]}$ 为对角线 $\text{[math]}$ 上的一个动点，则下列线段的长等于 $\text{[math]}$ 最小值的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

7. (2024八上·余江月考) $\text{[math]}$ 的立方根是．

答案解析收藏纠错 + 选题

三、填空题

8. (2019·吉安模拟) 3月5日，第十三届全国人大二次会议上国务院总理李克强在《政府工作报告》中指出：过去的一年里中国的精准脱贫推进有力，农村贫困人口减少1386万．其中数据13860000用科学记数法表示为．

答案解析收藏纠错 + 选题
9. (2019·吉安模拟) 夏季来临，某超市试销A、B两种型号的风扇，两周内共销售30台，销售收入5300元，A型风扇每台200元，B型风扇每台150元，问A、B两种型号的风扇分别销售了多少台？若设A型风扇销售了x台，B型风扇销售了y台，则根据题意列出方程组．

答案解析收藏纠错 + 选题
10. (2019八下·镇江期中) 如图，将△ABC绕点A按逆时针方向旋转100°，得到△AB₁C₁ ，若点B₁在线段BC的延长线上，则∠BB₁C₁的大小是度.

答案解析收藏纠错 + 选题
11. (2019·吉安模拟) 在平面直角坐标系中，一个智能机器人接到如下指令：从原点O出发，按向右，向上，向右，向下的方向依次不断移动，每次移动1m ．其行走路线如图所示，第1次移动到A₁ ，第2次移动到A₂…，第n次移动到A_n ，则△OA₂A₂₀₁₉的面积是．

答案解析收藏纠错 + 选题
12. (2024八下·宁津月考) Rt△ABC中，∠ABC=90°，AB=3，BC=4，过点B的直线把△ABC分割成两个三角形，使其中只有一个是等腰三角形，则这个等腰三角形的面积是．

答案解析收藏纠错 + 选题

四、解答题

13. (2019·吉安模拟)
1. （1）解不等式组： $\text{[math]}$
2. （2）如图，将△ABC沿BC方向平移2cm得到△DEF ，若△ABC的周长为16cm ，求四边形ABFD的周长．
答案解析收藏纠错 + 选题
14. (2019·吉安模拟) 先化简，再求值：（xy²+x²y）× $\text{[math]}$ ，其中x=π⁰﹣（ $\text{[math]}$ ）^﹣¹ ， y=2sin45°﹣ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2019·吉安模拟) 在不透明的袋子中有四张标着数字1，2，3，4的卡片，这些卡片除数字外都相同．小芸同学按照一定的规则抽出两张卡片，并把卡片上的数字相加．如图是她所画的树状图的一部分．
1. （1）由如图分析，小芸的游戏规则是：从袋子中随机抽出一张卡片后（填“放回”或“不放回”），再随机抽出一张卡片；
2. （2）帮小芸完成树状图；
3. （3）求小芸两次抽到的数字之和为奇数的概率．
答案解析收藏纠错 + 选题
16. (2019·上饶模拟) 图①、图②都是由边长为1的小菱形构成的网格，每个小菱形的顶点称为格点．点O ， M ， N ， A ， B均在格点上，请仅用无刻度直尺在网格中完成下列画图．
1. （1）在图①中，画出∠MON的平分线OP；
2. （2）在图②中，画一个Rt△ABC ，使点C在格点上．
答案解析收藏纠错 + 选题
17. (2020九上·芦淞期末) 如图为放置在水平桌面上的台灯的平面示意图，灯臂AO长为40cm，与水平面所形成的夹角∠OAM为75°．由光源O射出的边缘光线OC，OB与水平面所形成的夹角∠OCA，∠OBA分别为90°和30°，求该台灯照亮水平面的宽度BC（不考虑其他因素，结果精确到0.1cm．温馨提示：sin75°≈0.97，cos75°≈0.26， $\text{[math]}$ ）．

答案解析收藏纠错 + 选题
18. (2020七上·泾源期末) 目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利，初二数学小组在校内对“你最认可的四大新生事物”进行了调查，随机调查了 $\text{[math]}$ 人（每名学生必选一种且只能从这四种中选择一种）并将调查结果绘制成如下不完整的统计图．
1. （1）根据图中信息求出 $\text{[math]}$ =， $\text{[math]}$ =；
2. （2）请你帮助他们将这两个统计图补全；
3. （3）根据抽样调查的结果，请估算全校2000名学生种，大约有多少人最认可“微信”这一新生事物？
答案解析收藏纠错 + 选题
19. (2020·中宁模拟) 如图，已知AB是⊙O上的点，C是⊙O上的点，点D在AB的延长线上，∠BCD=∠BAC．
1. （1）求证：CD是⊙O的切线；
2. （2）若∠D=30°，BD=2，求图中阴影部分的面积．
答案解析收藏纠错 + 选题
20. (2019·吉安模拟) 在某水果店一次性购买A种水果的单价y（元）与购买量x（千克）的函数关系如图．
1. （1）下列关于三段函数图象的说法不正确是（）
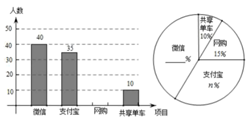
  A、第①段函数图象表示数量不多于5千克时，单价为10元．
  
  B、第③段函数图象表示数量不少于11千克时，单价为8.8元．
  
  C、第②段函数图象可知：当一次性数量多于5千克但不多于11千克时，每多买1千克，单价就降低1.2元．
2. （2）求图中第②段函数图象的解析式，并指出x的取值范围．
3. （3）某天老李计划用90元去该店买A种水果，问老李一次性（或最多）能买回多少千克A种水果？
答案解析收藏纠错 + 选题
21. (2020八下·遂平期中) 已知：如图，正比例函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$
1. （1）试确定上述正比例函数和反比例函数的表达式；
2. （2）根据图象回答，在第一象限内，当 $\text{[math]}$ 取何值时，反比例函数的值大于正比例函数的值？
3. （3） $\text{[math]}$ 是反比例函数图象上的一动点，其中 $\text{[math]}$ 过点 $\text{[math]}$ 作直线 $\text{[math]}$ 轴，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ；过点 $\text{[math]}$ 作直线 $\text{[math]}$ 轴交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ．当四边形 $\text{[math]}$ 的面积为6时，请判断线段 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系，并说明理由．
答案解析收藏纠错 + 选题
22. (2019·吉安模拟) 如图，抛物线C₁与抛物线C₂与x轴有相同的交点M ， N（点M在点N的左侧），与x轴的交点分别为A ， B ，且点A的坐标为（0，﹣3），抛物线C₂的解析式为y＝mx²+4mx﹣12m（m＞0）．
1. （1）求M ， N两点的坐标；
2. （2）在第三象限内的抛物线C₁上是否存在一点P ，使得△PAM的面积最大，若存在，求出△PAM的面积的最大值；若不存在，说明理由；
3. （3）设抛物线C₂的顶点为点D ，顺次连接A ， D ， B ， N ，若四边形ADBN是平行四边形，求m的值．
答案解析收藏纠错 + 选题
23. (2019·吉安模拟) 我们定义：如果一个三角形一条边上的高等于这条边，那么这个三角形叫做“等高底”三角形，这条边叫做这个三角形的“等底”．
1. （1）概念理解：
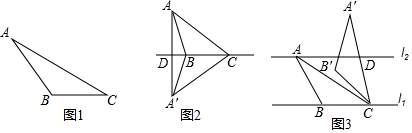
  如图1，在△ABC中，AC＝6，BC＝3，∠ACB＝30°，试判断△ABC是否是”等高底”三角形，请说明理由．
2. （2）问题探究：
  如图2，△ABC是“等高底”三角形，BC是”等底”，作△ABC关于BC所在直线的对称图形得到△A'BC ，连结AA′交直线BC于点D ．若点B是△AA′C的重心，求 $\text{[math]}$ 的值．
3. （3）应用拓展：
  如图3，已知l₁∥l₂ ， l₁与l₂之间的距离为2．“等高底”△ABC的“等底”BC在直线l₁上，点A在直线l₂上，有一边的长是BC的 $\text{[math]}$ 倍．将△ABC绕点C按顺时针方向旋转45°得到△A'B'C ， A′C所在直线交l₂于点D ．求CD的值．
答案解析收藏纠错 + 选题