江西省九江市赣北中考联盟2019年中考数学模拟考试试卷

更新时间：2020-04-29 浏览次数：210 类型：中考模拟

一、单选题

1. (2020七上·平邑期末) ﹣2的绝对值是（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019·九江模拟) 下列计算正确是（）

A . $\text{[math]}$ B . （a﹣b）²＝a²﹣b² C . a²+a³＝a⁵ D . （2a²b³）³＝﹣6a⁶b³

答案解析收藏纠错 + 选题
3. (2019·九江模拟) 下列图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2019·九江模拟) 小明用手机软件记录了最近30天的运动步数，并将记录结果制作成了如下统计表：

步数/万步

1.1

1.2

1.3

1.4

1.5

天数

3

9

5

a

b

小明这30天平均每天走1.3万步，在每天所走的步数中，众数和中位数分别是（）

A . 1.3，1.3 B . 1.4，1.3 C . 1.4，1.4 D . 1.3，1.4

答案解析收藏纠错 + 选题
5. (2019·九江模拟) 如图是二次函数 $\text{[math]}$ 的图象，有下面四个结论： $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ，其中正确结论是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2019·九江模拟) 如图，正方形ABCD中，AB＝3，点E是对角线AC上的一点，连接DE ，过点E作EF⊥DE ，交AB于点F ，连接DF交AC于点G ，下列结论：
①DE＝EF；②∠ADF＝∠AEF；③DG²＝GE•GC；④若AF＝1，则EG＝ $\text{[math]}$ ，其中结论正确个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题

7. (2024九下·金凤模拟) 分解因式： $\text{[math]}$ $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2019·九江模拟) 2019年3月5日召开十三届全国人大二次会议，政府工作报告中提到2012年我国的贫困人口为9899万人，2018年减少到1660万人，连续6年平均每年减贫1300多万人，将数据1300万用科学记数法可表示为．

答案解析收藏纠错 + 选题
9. (2019·九江模拟) 已知a ， b是一元二次方程x²+x﹣4＝0的两个不相等的实数根，则a²﹣b＝．

答案解析收藏纠错 + 选题
10. (2019·九江模拟) 《孙子算经》是中国古代重要的数学著作，成书于约一千五百年前，其中有首歌谣：“今有竿不知其长，量得影长一丈五尺，立一标杆，长一尺五寸，影长五寸，问竿长几何？”意思就是：有一根竹竿不知道有多长，量出它在太阳下的影子长一丈五尺，同时立一根一尺五寸的小标杆（如图所示），它的影长五寸（提示：1丈＝10尺，1尺＝10寸），则竹竿的长为．

答案解析收藏纠错 + 选题
11. (2019·九江模拟) 如图，在平面直角坐标系xOy中，等边△AOB的边长为10，点C在边OA上，点D在边AB上，且OC＝3BD ．反比例函数y＝ $\text{[math]}$ （k≠0）的图象恰好经过C、D两点，则k的值为．

答案解析收藏纠错 + 选题
12. (2019·九江模拟) 如图，已知△ABC中，AB＝AC＝5，BC＝8，将△ABC沿射线BC方向平移m个单位得到△DEF，顶点A，B，C分别与D，E，F对应，若以A，D，E为顶点的三角形是等腰三角形，且AE为腰，则m的值是．

答案解析收藏纠错 + 选题

三、解答题

13. (2019·九江模拟)
1. （1）先化简 $\text{[math]}$ ，再选择一个合适的x值代入求值．
2. （2）如图所示，已知点A ， D ， B ， E在同一条直线上，且AD＝BE ， BC＝EF ， ∠ABC＝∠DEF ，求证：AC∥DF ．
答案解析收藏纠错 + 选题
14. (2019·九江模拟) 解不等式组： $\text{[math]}$ 并将该不等式的解集在数轴上表示出来．

答案解析收藏纠错 + 选题
15. (2019·九江模拟) 如图，在▱ABCD中，点E为边BC上的中点，请仅用无刻度的直尺，按要求画图（保留画图痕迹，不写画法）．
1. （1）在图1中，作EF∥AB交AD于点F；
2. （2）在图2中，若AB＝BC ，作一矩形，使得其面积等于▱ABCD的一半．
答案解析收藏纠错 + 选题
16. (2021九上·萧县期末) 为了响应国家有关开展中小学生“课后服务”的政策，某学校课后开设了A：课后作业辅导、B：书法、C：阅读、D：绘画、E：器乐，五门课程供学生选择；其中A（必选项目），再从B、C、D、E中选两门课程．
1. （1）若学生小玲第一次选一门课程，直接写出学生小玲选中项目E的概率；
2. （2）若学生小强和小明在选项的过程中，第一次都是选了项目E ，那么他俩第二次同时选择书法或绘画的概率是多少？请用列表法或画树状图的方法加以说明并列出所有等可能的结果．
答案解析收藏纠错 + 选题
17. (2019·九江模拟)
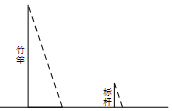
如图，在平面直角坐标系中，直线AB与x轴交于点B，与y轴交于点A，与反比例函数y= $\text{[math]}$ 的图象在第二象限交于点C，CE⊥x轴，垂足为点E，tan∠ABO= $\text{[math]}$ ，OB=4，OE=2．
1. （1）求反比例函数的解析式；
2. （2）若点D是反比例函数图象在第四象限上的点，过点D作DF⊥y轴，垂足为点F，连接OD、BF．如果S_△_BAF=4S_△_DFO ，求点D的坐标．
答案解析收藏纠错 + 选题
18. (2020·唐河模拟) 为更精准地关爱留守学生，某学校将留守学生的各种情形分成四种类型：A．由父母一方照看；B．由爷爷奶奶照看；C．由叔姨等近亲照看；D．直接寄宿学校．某数学小组随机调查了一个班级，发现该班留守学生数量占全班总人数的20%，并将调查结果制成如下两幅不完整的统计图．
1. （1）该班共有名留守学生，B类型留守学生所在扇形的圆心角的度数为；
2. （2）将条形统计图补充完整；
3. （3）已知该校共有2400名学生，现学校打算对D类型的留守学生进行手拉手关爱活动，请你估计该校将有多少名留守学生在此关爱活动中受益？
答案解析收藏纠错 + 选题
19. (2019·九江模拟) 如图（1）是一款手机支架，忽略支管的粗细，得到它的简化结构图如图（2）所示．已知支架底部支架CD平行于水平面，EF⊥OE ， GF⊥EF ，支架可绕点O旋转，OE＝20cm ， EF＝20 $\text{[math]}$ cm ．如图（3）若将支架上部绕O点逆时针旋转，当点G落在直线CD上时，测量得∠EOG＝65°．
1. （1）求FG的长度（结果精确到0.1）；
2. （2）将支架由图（3）转到图（4）的位置，若此时F、O两点所在的直线恰好于CD垂直，点F的运动路线的长度称为点F的路径长，求点F的路径长．
  （参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14，1.73）
答案解析收藏纠错 + 选题
20. (2024九下·上高模拟) 如图，⊙O是△ABC的外接圆，∠C＝60°，AD是⊙O的直径，Q是AD延长线上的一点，且BQ＝AB ．
1. （1）求证：BQ是⊙O的切线；
2. （2）若AQ＝6．
  ①求⊙O的半径；
  
  ②P是劣弧AB上的一个动点，过点P作EF∥AB ， EF分别交CA、CB的延长线于E、F两点，连接OP ，当OP和AB之间是什么位置关系时，线段EF取得最大值？判断并说明理由．
答案解析收藏纠错 + 选题
21. (2023·五河模拟) 为拓宽学生视野，我市某中学决定组织部分师生去庐山西海开展研学旅行活动，在参加此次活动的师生中，若每位老师带17个学生，还剩12个学生没人带；若每位老师带18个学生，就有一位老师少带4个学生．为了安全，既要保证所有师生都有车坐，又要保证每辆客车上至少要有2名老师．现有甲、乙两种大客车，它们的载客量和租金如表所示．

甲种客车

乙种客车

载客量/（人/辆）

30

42

租金/（元/辆）

300

400
1. （1）参加此次研学旅行活动的老师和学生各有多少人？租用客车总数为多少辆？
2. （2）设租用x辆乙种客车，租车总费用为w元，请写出w与x之间的函数关系式；
3. （3）在（2）的条件下，学校计划此次研学旅行活动的租车总费用不超过3100元，租用乙种客车不少5辆，你能得出哪几种不同的租车方案？其中哪种租车方案最省钱？请说明理由．
答案解析收藏纠错 + 选题
22. (2019·九江模拟) 已知二次函数y＝ax²﹣2ax﹣2的图象（记为抛物线C₁）顶点为M ，直线l：y＝2x﹣a与x轴，y轴分别交于A ， B ．
1. （1）对于抛物线C₁ ，以下结论正确是；
  ①对称轴是：直线x＝1；②顶点坐标（1，﹣a﹣2）；③抛物线一定经过两个定点．
2. （2）当a＞0时，设△ABM的面积为S ，求S与a的函数关系；
3. （3）将二次函数y＝ax²﹣2ax﹣2的图象C₁绕点P（t ， ﹣2）旋转180°得到二次函数的图象（记为抛物线C₂），顶点为N ．
  ①当﹣2≤x≤1时，旋转前后的两个二次函数y的值都会随x的增大而减小，求t的取值范围；
  
  ②当a＝1时，点Q是抛物线C₁上的一点，点Q在抛物线C₂上的对应点为Q'，试探究四边形QMQ'N能否为正方形？若能，求出t的值，若不能，请说明理由．
答案解析收藏纠错 + 选题
23. (2019·九江模拟) 【操作发现】
如图①，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．
1. （1）请按要求画图：将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连接BB′；
2. （2）在（1）所画图形中，∠AB′B=．
答案解析收藏纠错 + 选题