如图所示,AB为 圆弧轨道,BC为水平直轨道,圆弧的半径为R,BC的长度也是R.一质量为m的物体,与两个轨道的动摩擦因数都为μ,当它由轨道顶端A从静止下滑时,恰好运动到C处停止,那么物体在AB段克服摩擦力做功为( )
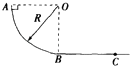
如图所示为四分之一圆柱体OAB的竖直截面,半径为R,在B点上方的C点水平抛出一个小球,小球轨迹恰好在D点与圆柱体相切,OD与OB的夹角为60°,则C点到B点的距离为( )
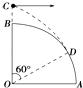
在水平粗糙的地面上使一物体由静止开始作匀加速运动,如图所示,第一次是拉力,第二次是用推力,两种情况下力的作用线与水平方向夹角、力的大小、位移大小均相同,那么比较两种情况,则下列说法正确的是( )

内壁光滑的环形凹槽半径为R,固定在竖直平面内,一根长度为 R的轻杆,一端固定有质量m的小球甲,另一端固定有质量为2m的小球乙.现将两小球放入凹槽内,初始时刻小球乙位于凹槽的最低点(如图所示),由静止释放后( )

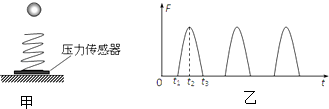
在用打点计时器验证机械能守恒定律的实验中,使质量为m=1.00kg的重物自由下落,打点计时器在纸带上打出一系列的点,选取一条符合实验要求的纸带如图所示.O为第一个点,A、B、C为从合适位置开始选取的三个连续点(其他点未画出).已知打点计时器每隔0.02s打一个点,当地的重力加速度为9.8m/s2 , 那么
如图所示,一传送带与水平面的夹角为30°,以v0=2m/s的初速度按图示方向匀加速1s后再做匀速运动,加速时的加速度为1m/s2 . 现将一质量为10kg的质点小工件轻放于传送带底端皮带,经一段时间后送到高2m的平台上,工件与传送带间的动摩擦因数为μ= ,取g=10m/s2 . 求:电动机由于传送工件多消耗的电能.

据动能定理﹣mgL(cos30°﹣cos60°)+qEL(sin60°﹣sin30°)= mv2﹣0
你认为王明同学求解等式是否正确?(回答“是”或“否”)