湖州市吴兴区2018-2019学年七年级下学期数学期末考试试...

更新时间：2020-07-09 浏览次数：501 类型：期末考试

一、选择题

1. (2019七下·吴兴期末) 分式 $\text{[math]}$ 有意义，则x的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019七下·吴兴期末) 已知：如图，直线a，b被直线c所截，且a∥b.若∠1=70°，则∠2的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022七下·绍兴期中) 下列计算结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2019七下·吴兴期末) 世界上最小的开花结果植物是澳大利亚的出水浮萍，它的果实像一粒微小的无花果，质量只有0.00000007g的，这个数值用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021七下·北仑期中) 下列因式分解正确的是（　　）

A . a²+8ab+16b²=（a+4b）² B . a⁴﹣16=（a²+4）（a²﹣4） C . 4a²+2ab+b²=（2a+b）² D . a²+2ab﹣b²=（a﹣b）²

答案解析收藏纠错 + 选题
6. (2021七下·镇海期末) 端午节放假后，赵老师从七年级650名学生中随机抽查了其中50名学生的数学作业，发现有5名学生的作业不合格，下面判断正确的是（）

A . 赵老师采用全面调查方式 B . 个体是每名学生 C . 样本容量是650 D . 该七年级学生约有65名学生的作业不合格

答案解析收藏纠错 + 选题
7. (2021七下·北仑期中) 若x²+2（2p﹣3）x+4是完全平方式，则p的值等于（）

A . $\text{[math]}$ B . 2 C . 2或1 D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2019七下·吴兴期末) 使得分式 $\text{[math]}$ 的值为零时，x的值是（）

A . x=4 B . x=-4 C . x=4或x=-4 D . 以上都不对

答案解析收藏纠错 + 选题
9. (2019七下·吴兴期末) 如图，直线 $\text{[math]}$ ， $\text{[math]}$ 表示一条河的两岸，且 $\text{[math]}$ ∥ $\text{[math]}$ 现要在这条河上建一座桥（桥与河的两岸相互垂直），使得从村庄A经桥过河到村庄B的路程最短，应该选择路线（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2019七下·吴兴期末) 已知关于x，y的方程组 $\text{[math]}$ 以下结论：①当x=1，y=2时，k=3；②当k=0，方程组的解也是y-x= $\text{[math]}$ 的解；③存在实数k，使x+y=0；④不论k取什么实数，x+9y的值始终不变，其中正确的是（）

A . ②③ B . ①②③ C . ②③④ D . ①②③④

答案解析收藏纠错 + 选题

二、填空题

11. (2024八下·吉安期中) 因式分解：a²﹣3a=

答案解析收藏纠错 + 选题
12. (2019七下·吴兴期末) 对某班组织的一次考试成绩进行统计，已知80.5～90.5分这一组的频数是7，频率是0.2，那么该班级的人数是人．

答案解析收藏纠错 + 选题
13. (2019七下·吴兴期末) $\text{[math]}$ = $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2019七下·吴兴期末) 若多项式x²-mx+n（m、n是常数）分解因式后，有一个因式是x-3，则3m-n的值为.

答案解析收藏纠错 + 选题
15. (2019七下·吴兴期末) 如图，将一条两边平行的纸带折叠，当∠2=80°，则∠1=.

答案解析收藏纠错 + 选题
16. (2019七下·吴兴期末) 六张形状大小完全相同的小长方形卡片，分两种不同形式不重叠的放在一个底面长为m，宽为n的长方形盒子底部（如图①、图②），盒子底面未被卡片覆盖的部分用阴影表示，设图①中阴影图形的周长为 $\text{[math]}$ ，图②中两个阴影部分图形的周长和为 $\text{[math]}$ 则用含m、n的代数式 $\text{[math]}$ =， $\text{[math]}$ =，若 $\text{[math]}$ ，则m=（用含n的代数式表示）

答案解析收藏纠错 + 选题

三、解答题

17. (2019七下·吴兴期末) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2019七下·吴兴期末)
1. （1）解分式方程： $\text{[math]}$ ；
2. （2）解二元一次方程组 $\text{[math]}$
答案解析收藏纠错 + 选题
19. (2023七下·东阳期末) 化简，再求值： $\text{[math]}$ ，再从-2，-1，0，1，2选择一个你喜欢的数代入求值.

答案解析收藏纠错 + 选题
20. (2021七下·柯桥期中) 已知：如图，AB∥CD，DE∥BC.
1. （1）判断∠B与∠D的数量关系，并说明理由.
2. （2）若∠B=（105-2x）°，∠D=（5x+15）°，求∠B的度数.
答案解析收藏纠错 + 选题
21. (2019七下·吴兴期末) 某校5月组织了学生参加“学习强国”知识竞赛，从中抽取了部分学生成绩（满分为100分）进行统计，绘制如下不完整的频数直方图，若将频数直方图划分的五组从左至右依次记为A、B、C、D、E，绘制如下扇形统计图，请你根据图形提供的信息，解答下列问题：
1. （1）频数分布直方图中，求A组的频数a，并补全频数直方图；
2. （2）扇形统计图中，D部分所占的圆心角n=度；
3. （3）若成绩在80分以上为优秀，全校共有2000名学生，估计成绩优秀的学生有多少名？
答案解析收藏纠错 + 选题
22. (2019七下·吴兴期末) 湖州奥体中心是一座多功能的体育场，目前体育场内有一块长80m，宽60m的长方形空地，体育局希望将其改建成花园小广场，设计方案如图，阴影区域是面积为192平方米的绿化区（四块相同的直角三角形），空白区域为活动区，且四周出口宽度一样.
1. （1）体育局先对四个绿化区域进行绿化，在完成工作量的 $\text{[math]}$ 后，施工方进行了技术改进，每天的绿化面积是原计划的两倍，结果提前四天完成四个绿化区域的改造，问原计划每天绿化多少平方米？
2. （2）老师提出了一个问题：你能不能求出活动区的出口宽度是多少呢？
  
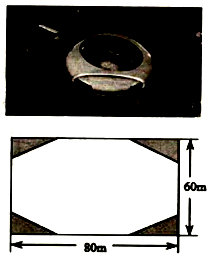
  请你根据小丽的方法求出活动区的出口宽度，并把过程写下来.
答案解析收藏纠错 + 选题
23. (2019七下·吴兴期末) （阅读理解）
我们知道，1+2+3+…+n= $\text{[math]}$ ，那么1²+2²+3²+…+n²结果等于多少呢？

在图1所示三角形数阵中，第1行圆圈中的数为1，即1² ，第2行两个圆圈中数的和为2+2，即2² ， …；第n行n个圆圈中数的和为 $\text{[math]}$ ，即n² ，这样，该三角形数阵中共有 $\text{[math]}$ 个圆圈，所有圆圈中数的和为1²+2²+3²+…+n².
1. （1）（规律探究）
  将三角形数阵经两次旋转可得如图2所示的三角形数阵，观察这三个三角形数阵各行同一位置圆圈中的数（如第n﹣1行的第一个圆圈中的数分别为n﹣1，2，n），发现每个位置上三个圆圈中数的和均为，由此可得，这三个三角形数阵所有圆圈中数的总和为：3（1²+2²+3²+…+n²）=，因此，1²+2²+3²+…+n²=.
2. （2）（解决问题）
  根据以上发现，计算： $\text{[math]}$ 的结果为.
答案解析收藏纠错 + 选题
24. (2019七下·吴兴期末) 阅读下面材料：
1. （1）小亮遇到这样问题：如图1，已知AB∥CD，EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现：过点O作OP∥AB，通过构造内错角，可使问题得到解决.
  请回答：∠O、∠BEO、∠DFO三个角之间的数量关系是.
2. （2）如图2，将△ABC沿BA方向平移到△DEF（B、D、E共线），∠B=50°，AC与DF相交于点G，GP、EP分别平分∠CGF、∠DEF相交于点P，求∠P的度数；
3. （3）如图3，直线m∥n，点B、F在直线m上，点E、C在直线n上，连接FE并延长至点A，连接BA、BC和CA，做∠CBF和∠CEF的平分线交于点M，若∠ADC=α，则∠M=（直接用含α的式子表示）.
答案解析收藏纠错 + 选题