初中数学苏科版九年级上册3.4方差同步练习

更新时间：2020-11-04 浏览次数：213 类型：同步测试

一、单选题

1. (2023八下·宝清期末) 如果将一组数据中的每个数都减去5，那么所得的一组新数据（）

A . 众数改变，方差改变 B . 众数不变，平均数改变 C . 中位数改变，方差不变 D . 中位数不变，平均数不变

答案解析收藏纠错 + 选题
2. (2020九上·长兴开学考) 甲、乙、丙、丁四名学生近5次数学成绩的平均数都是110分，方差如表，则这四名学生成绩最稳定的是（）

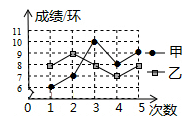
学生

甲

乙

丙

丁

方差(s²)

11.6

6.8

7.6

2.8

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
3. (2024九下·巴林左旗期中) 对于一组数据 $\text{[math]}$ ，下列说法正确的是（）

A . 中位数是5 B . 众数是7 C . 平均数是4 D . 方差是3

答案解析收藏纠错 + 选题
4. (2024·正定模拟) 某校九年级进行了3次数学模拟考试，甲、乙、丙、丁4名同学3次数学成绩的平均分都是129分，方差分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则这4名同学3次数学成绩最稳定的是（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
5. (2024九下·青岛期中) 八年级某学生在一次户外活动中进行射击比赛，七次射击成绩依次为（单位：环）：4，5，6，6，6，7，8．则下列说法错误的是（）

A . 该组成绩的众数是6环 B . 该组成绩的中位数数是6环 C . 该组成绩的平均数是6环 D . 该组成绩数据的方差是10

答案解析收藏纠错 + 选题
6. (2021八下·浦北期末) 如图是甲、乙两名射击运动员某节训练课的5次射击成绩的折线统计图，下列判断正确的是（）

A . 乙的最好成绩比甲高 B . 乙的成绩的平均数比甲小 C . 乙的成绩的中位数比甲小 D . 乙的成绩比甲稳定

答案解析收藏纠错 + 选题
7. (2023七下·桐梓期末) 甲、乙、丙、丁四人参加训练，近期的10次百米测试平均成绩都是13.2s，方差如下表：

选手

甲

乙

丙

丁

方差(s²)

0.020

0.019

0.021

0.022

则这四人中发挥最稳定的是（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
8. (2020八下·曲靖期末) 在某校举行的“我的中国梦”演讲比赛中，10名参赛学生的成绩统计如图所示，对于这10名学生的参赛成绩，下列说法中正确的是（）

A . 平均数是80分 B . 众数是5 C . 中位数是80分 D . 方差是110

答案解析收藏纠错 + 选题
9. (2020八下·复兴期末) 2016年，某市发生了严重干旱，该市政府号召居民节约用水，为了解居民用水情况，在某小区随机抽查了10户家庭的月用水量，结果统计如图．则关于这10户家庭的月用水量，下列说法错误的是（）

A . 众数是6 B . 中位数是6 C . 平均数是6 D . 方差是0.5

答案解析收藏纠错 + 选题

10. (2020八下·龙江月考) 甲、乙两班举行电脑汉字输入比赛，参赛学生每分输入汉字的个数统计结果如下:

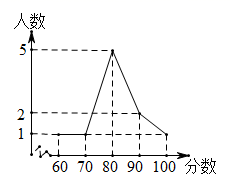
班级	参加人数	中位数	方差	平均数
甲	55	149	191	135
乙	55	151	110	135

某同学分析上表后得到下列结论：

①甲、乙两班学生平均成绩相同；

②乙班优秀的人数多于甲班优秀的人数（每分输入汉字个数≥150为优秀）；

③甲班成绩的波动比乙班大.

上述结论中正确的是（）

A . ①②③ B . ①② C . ①③ D . ②③

答案解析收藏纠错 + 选题

二、填空题

11. (2020·营口) 从甲、乙、丙三人中选拔一人参加职业技能大赛，经过几轮初赛选拔，他们的平均成绩都是87.9分，方差分别是S_甲²＝3.83，S_乙²＝2.71，S_丙²＝1.52.若选取成绩稳定的一人参加比赛，你认为适合参加比赛的选手是.

答案解析收藏纠错 + 选题
12. (2020·邵阳) 据统计：2019年，邵阳市在教育扶贫方面，共资助学生91.3万人次，全市没有一名学生因贫失学，其中，某校老师承担了对甲，乙两名学生每周“送教上门”的任务，以下是甲、乙两名学生某十周每周接受“送教上门”的时间（单位：小时）：
甲：7，8，8，9，7，8，8，9，7，9；

乙：6，8，7，7，8，9，10，7，9，9．

从接受“送教上门”的时间波动大小来看，学生每周接受送教的时间更稳定．（填“甲”或“乙”）

答案解析收藏纠错 + 选题
13. (2020·台州) 甲、乙两位同学在10次定点投篮训练中（每次训练投8个），各次训练成绩（投中个数）的折线统计图如图所示，他们成绩的方差分别为 $\text{[math]}$ 与 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ 填"＞”、“＝”、 “＜"中的一个）

答案解析收藏纠错 + 选题
14. (2020·宁波) 今年某果园随机从甲、乙、丙三个品种的枇杷树中各选了5棵，每棵产量的平均数 $\text{[math]}$ (单位：千克)及方差 $\text{[math]}$ (单位：千克²)如下表所示：

甲

乙

丙

$\text{[math]}$

45

45

42

$\text{[math]}$

1.8

2.3

1.8

明年准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植，则应选的品种.

答案解析收藏纠错 + 选题
15. (2020八下·凉山州期末) 已知一组数据x₁ ， x₂ ， …，x_n的方差为 $\text{[math]}$ ，则另一组数3x₁－2，3x₂－2，…，3x_n－2的方差为．

答案解析收藏纠错 + 选题
16. (2020八下·枣阳期末) 若一组数据2， $\text{[math]}$ ，4，3，3的平均数是3，则这组数据的中位数、众数、方差分别是.

答案解析收藏纠错 + 选题
17. (2020·平阳模拟) 某市多措并举，加强空气质量治理，空气质量达标天数显著增加，重污染天数逐年减少，越来越多的蓝天出现在人们的生活中.下图是该市4月1日至15日的空气质量指数趋势图，空气质量指数小于100表示空气质量为优良.

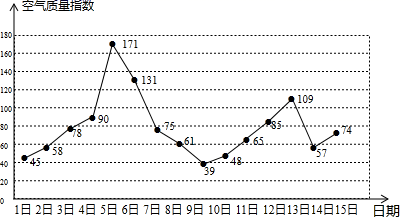
由上图信息，在该市4月1日至15日空气质量为优良的时间里，从第日开始，连续三天空气质量指数的方差最小.

答案解析收藏纠错 + 选题
18. (2020·咸阳模拟) 如图是一次射击训练中甲、乙两人的10次射击成绩的分布情况，则射击成绩的方差较小的是(填“甲”或“乙”).

答案解析收藏纠错 + 选题

三、解答题

19. (2020八下·番禺期末) 甲、乙两名射击运动员各进行10次射击，甲的成绩是7，7，8，9，8，9，10，9，9，9．乙的成绩如图所示（单位：环）
1. （1）分别计算甲、乙两人射击成绩的平均数；
2. （2）若要选拔一人参加比赛，应派哪一位？请说明理由．
答案解析收藏纠错 + 选题
20. (2019九上·温州月考) 为了考察甲、乙两种成熟期小麦的株高长势情况，现从中随机抽取6株，并测得它们的株高（单位：cm）如下表所示：

甲

63

66

63

61

64

61

乙

63

65

60

63

64

63

（Ⅰ）请分别计算表内两组数据的方差，并借此比较哪种小麦的株高长势比较整齐？

（Ⅱ）现将进行两种小麦优良品种杂交实验，需从表内的甲、乙两种小麦中，各随机抽取一株进行配对，以预估整体配对情况，请你用列表法或画树状图的方法，求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.

答案解析收藏纠错 + 选题

21. (2018八上·靖远期末) 某中学开展演讲比赛活动，八年级(1)班、八年级(2)班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩(满分100分)如下图：八年级(1)班成绩为条形统计图，八年级(2)班成绩为扇形统计图．

（1）根据上图填写下表

班别	平均数(分)	中位数(分)	众数(分)
八年级(1)班	85		85
八年级(2)班	85	80

（2）如果要在复赛成绩的十名选手中决定在同一班中选五名参加比赛活动，你认为哪个班实力更强一些？通过计算，说明理由．

答案解析收藏纠错 + 选题

22. (2017八下·汶上期末)
某商场统计了今年1～5月A，B两种品牌冰箱的销售情况，并将获得的数据绘制成折线统计图
1. （1）分别求该商场这段时间内A，B两种品牌冰箱月销售量的中位数和方差；
2. （2）根据计算结果，比较该商场1～5月这两种品牌冰箱月销售量的稳定性．
答案解析收藏纠错 + 选题
23. (2017八下·萧山期中)
某市甲、乙两个汽车销售公司，去年一至十月份每月销售同种品牌汽车的情况如图所示：
1. （1）请你根据上图填写下表.
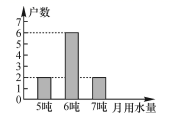
  销售公司
  平均数
  方差
  中位数
  众数
  甲
  
  9
  乙
  9
  17.0
  8
2. （2）请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析：①从平均数和方差结合看；②从折线图上甲、乙两个汽车销售公司销售数量的趋势看（分析哪个汽车销售公司较有潜力）．
答案解析收藏纠错 + 选题
24.
甲乙两支篮球队进行了5场比赛，比赛成绩绘制成了统计图（如图）
（1）分别计算甲乙两队5场比赛成绩的平均分．
（2）就这5场比赛，分别计算两队成绩的极差；
（3）就这5场比赛，分别计算两队成绩的方差；
（4）如果从两队中选派一支球队参加篮球锦标赛，根据上述统计，从平均分、极差、方差以及获胜场数这四个方面分别进行简要分析，你认为选派哪支球队参赛更能取得好成绩？

第一场
第二场
第三场
第四场
第五场
甲
82
86
95
91
96
乙
106
90
85
87
82

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

初中数学苏科版九年级上册3.4方差同步练习

副标题：

*注意事项：

初中数学苏科版九年级上册3.4方差同步练习

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

	第一场	第二场	第三场	第四场	第五场
甲	82	86	95	91	96
乙	106	90	85	87	82

学生	甲	乙	丙	丁
方差(s²)	11.6	6.8	7.6	2.8

选手	甲	乙	丙	丁
方差(s²)	0.020	0.019	0.021	0.022

	甲	乙	丙
$\text{[math]}$	45	45	42
$\text{[math]}$	1.8	2.3	1.8

小学

初中

高中

初中数学苏科版九年级上册3.4方差 同步练习

副标题：

*注意事项：

初中数学苏科版九年级上册3.4方差 同步练习

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

初中数学苏科版九年级上册3.4方差同步练习

初中数学苏科版九年级上册3.4方差同步练习